Courses
- Elements of Data Science – SDS 322E (course creator, coordinator)
- Elements of Statistis – SDS 320E
- Computational Biology and Bioinformatics – SDS 348
- Biostatistics – SDS 328M
- Data Analysis for the Health Sciences – SDS 302
- Cognition, Human Learning, and Motivation – ALD 320
Short Courses
- Bayesian Statistics — UT Summer Statistics Institute, 2020, 2021
- Introduction to Causal Inference — UT Summer Statistics Institute, 2019
- Introduction to Causal Inference — UT Summer Statistics Institute, 2018
Graduate-Level Courses (TA)
- Instructional Psychology – EDP 382D (Butler, Spring 2016)
- Complex Cognitive Processes – EDP 382D (Butler, Fall 2015)
- Social Psychology – EDP 381M (Falbo, Fall 2014)
Other Teaching and Tutoring
- GRE & GMAT Tutor – NextStep Test Prep (Austin TX, 2015-2018)
- Mathematics Instructor – Mathnasium (Austin TX, 2014-2015)
- SAT/ACT Tutor – Huntington Learning Center (Arlington TX, 2012-13)
- Long-Term Substitute – Birdville, Grapevine-Colleyville ISDs (2012-13)
- Library Research Assistant – Reed College Library (Portland OR, 2010-12)
Teaching Statement
Preface
I know what it is you are looking for here. As a teacher and educational researcher, I am minutely acquainted with “what works,” with common pitfalls, and with what’s en trend in teaching today. I remember when I first began teaching at the high school level and as part of the hiring process I had to sit through a long, timed, online TeacherInsight interview carefully designed to probe my inner pedagog. The items were well written and psychometrically sound, tapping dimensions like teacher expectations and student focus, with many positing a difficult trade-off (“Is it important for students to like you?”). My responses to such questions were compared to those of highly successful teachers and on this basis a score was computed representing my latent teacher quality.
Since that time, I have become a professional educator. I have read so much about the topic that I could rattle off a near-exhaustive list of evidence-based teacher practices that improve student outcomes: I could tell you about how I set explicit goals for my students based on clearly stated learning outcomes; I could tell you about how I take every opportunity to give them feedback about their progress and to seek feedback from them about my teaching in turn, ideally from their contributions to in-class discussions or other collaborative learning activity. I could give examples of how my inclusive classroom climate emphasizes the connection between effort and progress, perhaps with a story about how I turned a student’s error into an opportunity for learning resilience (or even better, grit). And all of this would satisfy the requirements of any hiring committee. Please understand that it is not my intention to make light of these extremely effective teaching practices! Countless researchers have dedicated their professional lives to evaluating educational interventions for increasing student achievement, and of course I make use of them in my classes: they work! I just wanted this all out in the open, because the task of writing such a personal document is unbearably stultifying when you imagine your readership is just checking off boxes in a rubric.
Instead of shaping my story so that it conforms to a list of best practices (I’ll more-or-less do that below!), let me get embarrassingly personal here right at the start and expand upon a few facets of myself that make my courses uniquely effective: I am contagiously excitable about everything, I am a latter-day transcendentalist who keeps the pursuit of truth, beauty, and goodness front-and-center, and because I cannot tolerate waste or inefficiency, I leverage innovations in technology and cognitive science to eliminate it from the classroom to optimize learning and to make the most of my students’ time.
People have always asked me why I am smiling, and when I was younger I never knew what to say. Did I need an excuse for being happy and kind? Like a rising tide, my unflagging positivity has always buoyed those around me; indeed, in middle school I was voted “friendliest”
Over the years, I have come to realize that my abiding good-cheer springs from a deep Love of Learning that infuses my every moment with excitement and personal meaning. For more on that, please see my About page!
See below for my Teaching Philosophy: a more rigorous, formalized, and practical statement of what being an educator at the college level means to me. Stay until the end to see why I feel that education in statistics is of the utmost importance!
Teaching Philosophy
In college, classes meet for just a few hours each week and, for better or worse, students are expected to assume greater responsibility for their own learning; as instructors, what takes place during our limited time with students requires our utmost care, having implications not just for these individuals but, because it helps shape them into the independent adults they will become, for our society as a whole. I know that making optimal use of this time means producing students who are more than merely knowledgeable, but who are knowledge-seeking and ultimately self-educating.
When I teach, I am guided by three main goals: to help students build domain knowledge and skills, to motivate them to pursue such knowledge for themselves, and to train them in the most effective strategies for learning. Factual knowledge, though necessary for laying a foundation for higher-order thinking,
Lamentably, the love of learning is seldom seen in our classrooms today. The traditions of the lecture hall create a gulf between teachers and students that has today become filled by a sea of glowing laptops; as a teacher I am ever mindful that while students may be physically present in class, they are in personal worlds of their own to which we rarely have access. Accessing those private realms of self-generated meaning is necessary for real education to occur, because it is here that learning literally changes students. But how? What individual students are experiencing in the classroom is almost completely invisible to us as teachers: we are not able to read minds, let alone be 100 places at once! My 10 years experience teaching and tutoring students on an individual basis has made this classroom reality extremely clear.
On the other hand, when I tutor, I can personally monitor my student’s understanding by asking questions to identify knowledge-gaps and I can respond with immediate feedback to fill them in; I can also adjust my instruction on an individual basis to give each student an appropriate challenge. And as it turns out, this one-on-one tutoring is an extremely effective way to learn: an oft-cited study boasts a 2 standard-deviation improvement over conventional classroom instruction covering the same material (Bloom, 1980). Furthermore, through the interpersonal back-and-forth of 1-on-1 tutoring, I really get to know the student as an individual, figuring out their goals and motivations (more on motivation below); as much as possible, we discuss with one another as equals, thus minimizing the unpleasant, autonomy-sapping power dynamic inherent in every teacher–learner situations that poisons so many students against reading, math, and many otherwise joyful portals to knowledge.
My constant aim as a teacher is to scale up these beneficial aspects of tutoring and infuse them into the lecture hall. I know that in large-format classes, lecturing is a fact of life, but an effective lecture is one that gets students actively engaged in the learning processes, and here I mean much more than mere note-taking. When I teach a large lecture-based course as I have for several years now, I punctuate my lectures with pertinent activities that break up the monotony and get students working with the material we just covered either individually or in small groups. While they work together on relevant, well-defined tasks, I make the rounds, checking in with students to get feedback about their understanding and offering my own supportive feedback in return. Finally, at the end of each lecture (or sometimes during), I give them each a low-stakes quiz over the day’s material. Not only does this hold students accountable for the lecture material, it also gives them the opportunity to practice applying the information they just learned. By focusing on getting students to demonstrate their understanding through active engagement, I can solicit feedback about my own teaching in real time …however much easier it may be to ask ”does that make sense?” and to accept a few nods from the front row as evidence of a job well done. By always trying to see the learning situation from the individual student’s point of view, the task of monitoring all students’ understanding—though still a Herculean undertaking in the best of cases—becomes much easier to manage.
The student’s point of view is even more important for another reason: Motivation! To motivate students to complete their assignments and to motivate them to actually learn and to enjoy learning for its own sake are two very different things! I have found that by being engaging and outgoing, by showing my passion for their subject matter, and by offering caring, human relationships to students through individual recognition, positive regard, and mutual respect, I can keep even the most academically aloof students engaged in the course. Fortunately, my subjective experience is backed by strong empirical evidence. For example, a recent meta-analysis examining how teacher–student relationships impact achievement (consisting of around 350,000 students and 15,000 teachers) reported an average effect size of 0.72, making it one of the most robust effects on achievement in the literature (Cornelius-White, 2007). It also revealed that the main reason students give for disliking school is that they do not like their instructor. Indeed, among drop-outs, around half say their classes where not interesting or exciting; sadder still, a full two-thirds of them say they felt that none of their teachers was interested in their individual success (Bridgeland, Dilulio, & Morison, 2006). This is yet another example of how lessons learned from tutoring have been invaluable for my classroom teaching: knowing students’ names, educational goals, and individual circumstances (to the degree that I am reasonably able) not only provides me with information about them, it acknowledges their individual humanity, lifting the veil of anonymity and turning lurkers into learners who listen to what you have to say because they hear it being said to them!
For all this talk about learning for its own sake, there has to be an uncompromising system of accountability in place for assessing exactly what learning is (or is not) taking place in college classrooms. High school students must sit for state exit exams, but because there is nothing analogous to these comprehensive assessments in higher education, the onus is on instructors to create final, cumulative performance metrics that accurately gauge students’ learning. A grade in the gradebook is thus a final verdict reached by a professor about student’s mastery of the the course; it should more than merely reflect a student’s past performance on one or two multiple-choice exams: it should be a promissory note, vouching for what a student knows about a subject and what a student is capable of doing on their own. A college education should give students knowledge and skills that can be flexibly applied outside of the classroom and that remain accessible to them over time; however—despite the common-sense belief that performance on test day will persist over time and transfer usefully into the “real-world”—there is no guarantee that students will remember this information, especially if they only look at it once right before the exam!
Students’ retention of information is a function of the quality of initial learning and the continued practice students get over time. Indeed, far from being a mere “assessment” of previously learning, testing itself has important benefits for memory of the material. By prompting students to repeatedly retrieve information from their memory and use it, frequent, cumulative testing is known to benefit both long-term retention of material and transfer of learning to new contexts, two important goals of education (Roediger & Butler, 2011). However, most courses are not designed in a way that facilitates frequent quizzing or revisiting previously covered topics; this is particularly true in higher education, where a small number of exams typically account for the bulk of a students grade. But not only does such a course design fail to take advantage of the mnemonic benefits of retrieval practice: it also creates a perverse incentive structure, rewarding behaviors that lead to transitory learning while penalizing those leading to durable learning. Cramming, though it results in much poorer long-term retention, can produce equivalent—indeed sometimes better—recall on an immediate (or next-day) test than does spacing out study sessions (e.g., Rawson & Kintsch, 2005). Thus, cramming is an effective way to pass high-stakes tests but a terrible way to achieve durable learning, and it is therefore incumbent on educators to incentivize long-term retention with things like cumulative assignments. I organize my courses to leverage the power of testing and spacing: instead of crammable, high-stakes exams, students take daily quizzes that are cumulative in nature and which account for the bulk of their grade. Not only do these quizzes keep students more consistently engaged in the course, they give them daily practice retrieving and using important material in order to better maintain this knowledge in the future.
To realize the full potential of cognitive science in the classroom, technology must be wedded with education once and for all. Computers can complete an instructor’s repertoire of superpowers by giving us that elusive ability to individualize instruction; they can help make teachers aware of what individual students are thinking, feeling, and understanding, allowing us to construct more meaningful educational experiences. The common perception of computer-based learning as rigid and programmatic is simply out of date. Just as self-driving cars monitor and adapt to changes in their environment, educational technologies are increasingly able to monitor and adapt to students. For example, intelligent tutoring systems use interactions with students to model students’ knowledge of a subject, to assign appropriately challenging content, to monitor students’ problem-solving steps, to provide context-sensitive feedback, to adapt the teaching strategy to students’ individual learning patterns, and to chart their progress toward a mastery criterion, all in real time. I have used tutoring systems and spaced-repetition software to administer homework activities to students in my courses, and I get a clear picture of how they are progressing and what they do and don’t know at any given time. Further, it also helps me predict the optimal time to revisit past material, which ensures its usefulness to students far into the future. For example, in the research I did for my Master’s degree, I developed a tool for taking student quiz data and determining the degree to which each person understands a given topic. This way, subsequent quizzes can be individualized by having each student revisit the topics they are weakest in by giving them additional questions about those topics and updating their predicted level of mastery based on their responses. And while this may sound complicated and time consuming, it is entirely automated: a unique quiz is automatically generated for each student to address any problem areas based on their previous performance.
By ending with a sober discussion of the mechanics of retention and the practicalities of the classroom, I hope that I haven’t overshadowed the core tenets of my teaching philosophy: the essence of education is empowering students to learn and helping them find joy and personal fulfillment in the learning process itself. This is the driving force that compels human beings to deal imaginatively and constructively with new experiences, and this is an absolute asset in a rapidly changing world. It has been prophesied that children now entering grade school will end up working in careers that havent even been invented yet. The internet, genomics, social media, smart phones…none of these developments were foreseeable fifteen years before their advent, and the pace of innovation continues to accelerate. With the newest textbooks and lesson plans becoming obsolete the moment they are printed, it is now certain that exactly what students are taught is far less important than how students learn to teach themselves. Leading young people to want to learn and giving them all the best tools with which to do so is only way were going to solve the problems we dont yet know exist, to answer questions yet unasked!
Why Math and Statistics?
Over my 10 years of teaching and tutoring experience (at 2 Texas ISDs, 2 universities, and 3 private tutoring companies), I have taught almost everything there is to teach. However, mathematics remains my cherished subject, and here’s why: From the time I had to memorize my times tables until I went off to college, I thought that math was the worst. Just totally boring drudgery. Never once was I excited by or interested in the subject, which to me meant repetitive calculations, unexplained formulas, and tedious rules.
Math lets us tame wild abstraction, organize disorder, explain the inexplicable. Because I earned my mathematical chops later in life and with no small personal effort—discovering the holes in my knowledge and finding ways to patch them, ways I wish I had been taught—all of the difficulties new learners encounter have been seared into my psyche. Unlike the mathematician-savant who, because she never experienced their same difficulties, cannot put herself in her students’ position, I can see math through the jaded, frustrated eyes of those I teach and I can empathize with them because their plight was my own.
Quantitative reasoning–including statistical and probabilistic thinking–is a skill that everyone needs but that very few actually have. The information age is bringing about a second Reformation: in the first, the printing press enabled individuals to draw conclusions based on their own reading of sacred texts. Literacy, a skill once reserved for learned monks, became a skill for everyone, breaking the Church’s monopoly on meaning. Today, we’re up to our ears in data and it’s all just a click away: now it is numeracy that is needed to democratize meaning! Our newspapers are filled not just with the written word, but with numbers and statistics which have become indispensable to society in countless ways: science, engineering, business, medicine… But as numbers have become the final arbiter in questions of truth, statistics has increasingly become the province of an expert few, a conclave of technocrats whose dogma is beyond reproach.
It is our duty as teachers to redress this. There is a dangerous tendency among those lacking statistical training to defer uncritically to the opaque models and formidiable language of experts. Loosely paraphrasing Bob Dylan, it is difficult to criticize what you don’t understand. This asymmetry cedes far too much power to far too few individuals and, if not always pernicious, feels fundamentally unegalitarian. I believe that many “advanced” (read: important) statistical topics can be made perfectly accessible to students early on in their education; students should be exposed to the beautiful foundations (and cutting-edge developments) of our modern decision-making machinery, not merely shown where to click as they go through the motions. Gaining appreciation for how statistical techniques actually work is not an empty academic exercise; rather, it prepares students for success in an increasingly computation-driven world.
Indeed, a lot of the most important aspects of the statistics curriculum are “hidden.” For example, learning to read statistical equations (interpreting coefficient estimates, calculating fitted values, understanding error) is a skill in its own right and needs practicing: statistical equations posit specific relationships among actual phenomena and thereby encode a model of the way things are. If you cannot criticially examine someone’s model-making, you are taking too much on faith! Humans are over-eager pattern-matchers, quick to draw a causal line between A and B; reading equations requires slowing down and deferring such judgement. This builds the discipline needed for cognitive reflection
Training in probability and statistics can make otherwise paradoxical concepts come to feel intuitive. Take, for example, regression to the mean: when things have gotten extremely bad, they are more likely to improve than to become still more extreme. If you are a business owner whose company is experiencing a slump, you may decide to pay for outside consulting help. If business starts to improve, you may be tempted to attribute it to the consulting, but things may have just improved on their own! (Once you understand it, you see examples everywhere: medicine, sports, etc.) Combine this with the ability to think asymptotically (imagining infinite repetitions or timescales), and other important lessons become self-evident. For example, markets fluctuate but returns are stable in the long-run.
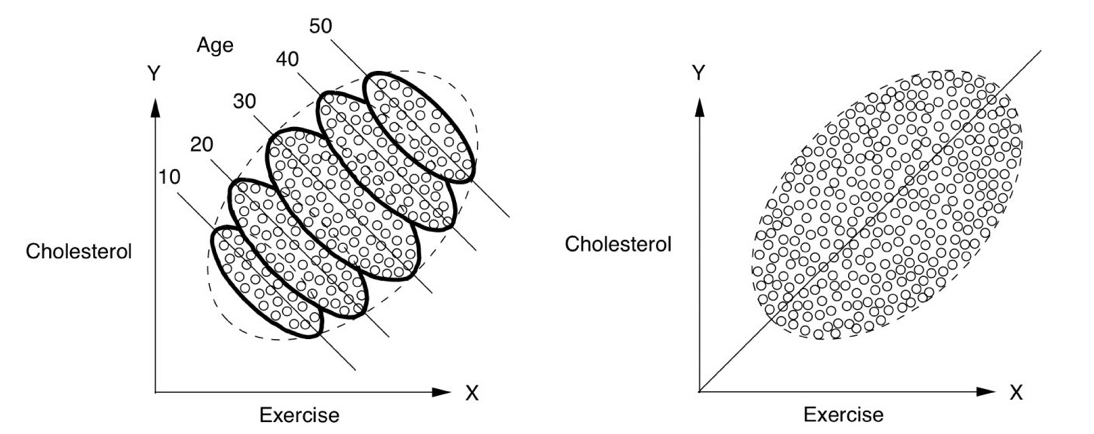
Sometimes a relationship that appears in several groups can disappear or reverse when the data is pooled together, something called Simpson’s paradox. Perhaps the relationship between cholesterol levels and hours of jogging is negative (more jogging, lower cholesterol) for several different age groups. However, if you combine the data together and no longer consider age group, the relationship between jogging and cholesterol may become positive (more jogging, higher cholesterol)! On inspection, this is because older people are more likely to jog and more likely to have higher cholesterol.
Learning statistics can also make you a better teacher yourself! Describing and visualizing data require taking an otherwise-impenetrable array of numbers, putting them into context, and summarizing them in human-intuitive ways. Putting information into context and making it intelligible to others is an important part of communicating information, which is itself a crucial part of teaching. Indeed, statistics is really the science of learning from data and teaching others about what you found! With contagious enthusiasm, a wealth of experience, and a great sense of purpose, I work to empower students not only to succeed in their coursework, but to value statistical thinking for its own sake and make use of it in their daily lives as informed and numerically savvy citizens.
No joke!
 ↩︎
↩︎For more, check out my RateMyProfessor page↩︎
Remembering information is, after all, the biggest and most basic level of Bloom’s famous pyramid!
 ↩︎
↩︎Drop a minus sign somewhere, you get the whole problem wrong! What, you don’t enjoy math?!↩︎
No one makes the case for improved mathematics education more lucidly than Paul Lockhart in his A Mathematician’s Lament. Do yourself a huge favor and stop to read this if you have any interest at all in math or teaching (and if you’ve read this far, you do)!↩︎
cf. this famous quote attributed to Karl Rove: “guys like [you are] in what we call the reality-based community, [people]”who believe that solutions emerge from your judicious study of discernible reality. […] That’s not the way the world really works anymore. We’re an empire now, and when we act, we create our own reality. And while you’re studying that reality—judiciously, as you will—we’ll act again, creating other new realities, which you can study too, and that’s how things will sort out. We’re history’s actors…and you, all of you, will be left to just study what we do."↩︎
In behavioral economics parlance, turning on System 2. Here are some examples: Do be careful!↩︎
All of which fall under the (somewhat nebulous) umbrella of “critical thinking”↩︎