#Correlation People are often interested in how different variables are related to each other. In general, a correlation is just a relationship or association between two variables. If one variable gives you information about the other, then they are correlated (dependent, associated). More commonly, we talk about two variables having a linear relationship. To understand linear relationships, it helps to have a good grasp of variance and covariance.
Variance is a number that quantifies how spread out a variable’s values are from their mean on average. We subtract the mean ˉx from each each observation xi, then we square each of these devations, and then average them up, to get the sample’s variance. (We divide by n−1 rather than n because we are assuming we have a sample of data from a larger population: see Bessel’s correction). Also, the standard deviation is just the square root of the variance: if the variance is the average squared deviation, the standard deviation represents the average deviation (though there are other, less common measures of this like average absolute deviation).
var(X)=∑i(xi−ˉx)2n−1sdx=√var(X)=√∑i(xi−ˉx)2n−1
Covariance is a measure of association between two variables: how much the larger values of one variable tend to “go with” larger values of the other variable (and how much smaller values go with with smaller values). When one value of one variable is above its mean, does the corresponding value for the other variable tend to be above its mean too? If so, you have positive covariance. In contrast, if one variable tends to have values above its mean when the other tends to have values below its mean, you have negative covariance. If there is no relationship between the deviations of each of the two variables from their respective means, the covariance will be zero.
For both variables x and y, we calculate the deviation of each observation from it’s mean, xi−ˉx and yi−ˉy. Then we multiply those deviations together, (xi−ˉx)(yi−ˉy), and we average these products across all observations.
cov(X,Y)=∑i(xi−ˉx)(yi−ˉy)n−1
The numerator is where the magic happens. If, for a point on your scatterplot (xi,yi), your xi is less than its mean (so xi−ˉx is negative), but your yi is greater than its mean (so yi−ˉy is positive), then the product of the two deviations in the summation will be negative.
For example, let’s say we observe these two data points:
xy1436ˉx=2ˉy=5
Then we have
∑(xi−ˉx)(yi−ˉy)n−1=(1−2)(4−5)+(3−2)(6−5)2−1=(−1)(−1)+(1)(1)1=2
These variables have a sample covariance of 2.
While the sign of the covariance will always tell you whether a relationship between to variables is positive or negative (i.e, relationship direction), the magnitude of the covariance can be misleading as a measure of relationship strength because it is influenced by the magnitude of each of the variables.
Let’s work with this a bit. Below we plot X and Y, which have a perfectly linear relationship; also, the slope is one (when X goes up by 12.5, Y goes up by 12.5). Along the margin, we show the distribution of each variable with tick marks. Focusing on one variable at a time, notice they are both uniformly distributed. We have also drawn through the mean of each variable (MX=50;MY=200). Notice also that both X and Y have the same number of data points (9), and that they are both evenly spaced throughout. Thus, they have the same standard deviation (SD=34.23). Now the sample covariance of X and Y is 1171.88, which is positive.
library(ggplot2)
library(dplyr)
#library(tidyr)
library(MASS)
#samples = 10
#r = 0.5
#data = as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE))
data<-data.frame(X=seq(0,100,length.out = 9),Y=seq(150,250,length.out = 9))
knitr::kable(round(data,3),align='cc')| X | Y |
|---|---|
| 0.0 | 150.0 |
| 12.5 | 162.5 |
| 25.0 | 175.0 |
| 37.5 | 187.5 |
| 50.0 | 200.0 |
| 62.5 | 212.5 |
| 75.0 | 225.0 |
| 87.5 | 237.5 |
| 100.0 | 250.0 |
ggplot(data,aes(X,Y))+geom_point()+geom_hline(yintercept=mean(data$Y))+geom_vline(xintercept=mean(data$X))+geom_rug(color="gray50")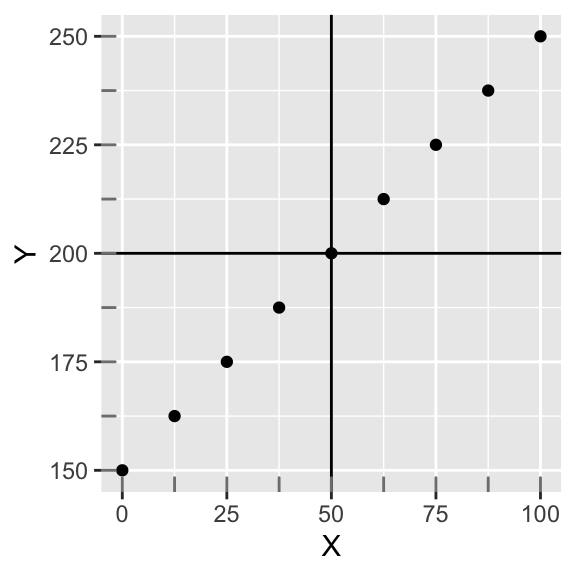
cov(data$X,data$Y)## [1] 1171.875But the number 1171.88 itself is rather arbitrary. It is influenced by the scale of each variable. For example, if we multiply both variables by 100, we get:
round(cov(10*data$X,10*data$Y))## [1] 117188We have arbitrarily increased the covariance by a factor of 100.
Here’s an interesting thought: this perfectly linear relationship should represent the maximum strength of association. What would we have to scale by if we wanted this pefect (positive) covariance to equal one?
Well, if we standardize both variables (by subtracting the variable’s mean from each observation and dividing that difference by the variable’s standard deviation), we preserve the relationship among observations but we put them on the same scale (i.e., each variable has a mean of 0 and a standard deviation of 1). That is, we convert each variable to a z-score (if you need a refresher, see my previous post about z-scores).
Plotting them yields an equivalent looking plot, but notice how the scales have changed! The relationship between X and Y is completely preserved. Also, the covariance of X and Y is now 1.
data<-data.frame(scale(data))
ggplot(data,aes(X,Y))+geom_point()+geom_hline(yintercept=mean(data$Y))+geom_vline(xintercept=mean(data$X))+geom_rug(color="gray50")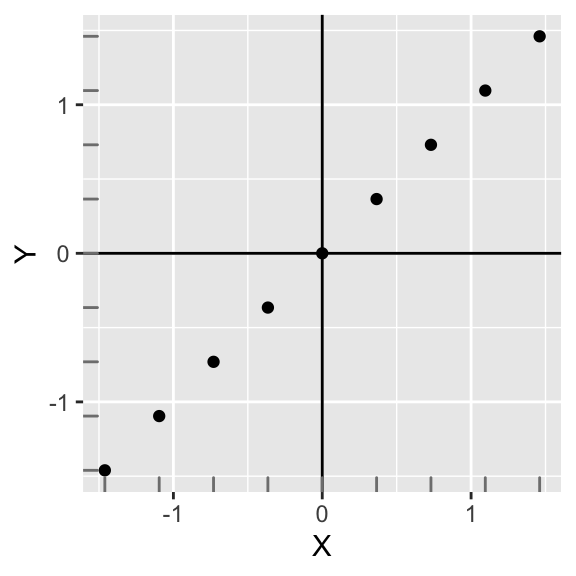
This is interesting! The covariance of two standardized variables that have a perfectly linear relationship is equal to 1. This is a desirable property: The linear relationship between X and Y simply cannot get any stronger!
Equivalently, since the calcualtion of the covariance (above) already subtracts the mean from each variable, instead of standardizing X and Y, we could just divide the original cov(X,Y) by the standard deviations of X and Y. Either way is fine!
r=∑iZXZYn−1=∑(xi−ˉx)(yi−ˉy)sdXsdY(n−1)=cov(X,Y)√var(X)√var(Y)=1171.8834.23×34.23=1
We have hit upon the formula for Pearson’s correlation coefficient (r) for measuring the strength of a linear association between two variables. Taking the covariance of two standardized variables will always yield r. In this case, r=1 indicating a perfect linear direct relationship between the variables. This is the maximum value of r (the minimum value is -1, indicating a perfectly linear inverse relationship). Also, r=0 means no relationship (i.e., random noise). Observe the scatterplots, and their respective correlations, below:
library(cowplot)
samples = 10; r = -1
d1 = as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE));r=-.5
d2= as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE));r=0
d3= as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE));r=.5
d4= as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE));r=1
d5= as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE))
names(d1)<-names(d2)<-names(d3)<-names(d4)<-names(d5)<-c("X","Y")
p1<-ggplot(d1,aes(X,Y))+geom_point()+theme(axis.text.x=element_blank(),axis.text.y=element_blank(),
axis.ticks=element_blank(),axis.title.x=element_blank(),axis.title.y=element_blank())+ggtitle("r = -1")
p2<-ggplot(d2,aes(X,Y))+geom_point()+theme(axis.text.x=element_blank(),axis.text.y=element_blank(),axis.ticks=element_blank(),axis.title.x=element_blank(),axis.title.y=element_blank())+ggtitle("r = -0.5")
p3<-ggplot(d3,aes(X,Y))+geom_point()+theme(axis.text.x=element_blank(),axis.text.y=element_blank(),axis.ticks=element_blank(),axis.title.x=element_blank(),
axis.title.y=element_blank())+ggtitle("r = 0")
p4<-ggplot(d4,aes(X,Y))+geom_point()+theme(axis.text.x=element_blank(),axis.text.y=element_blank(),axis.ticks=element_blank(),axis.title.x=element_blank(),axis.title.y=element_blank())+ggtitle("r = 0.5")
p5<-ggplot(d5,aes(X,Y))+geom_point()+theme(axis.text.x=element_blank(),axis.text.y=element_blank(),axis.ticks=element_blank(),axis.title.x=element_blank(),axis.title.y=element_blank())+ggtitle("r = 1")
plot_grid(p1,p2,p3,p4,p5,nrow=1)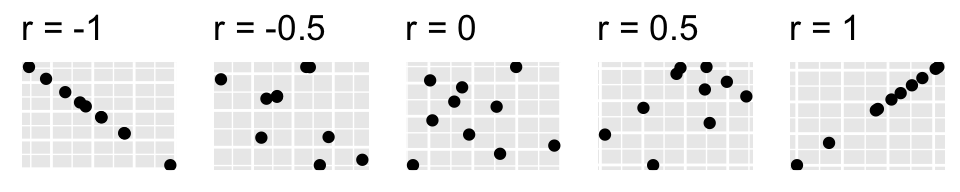
theme_set(theme_grey())Correlation demonstration!
Let’s approach the correlation r again, but from a slightly different angle. I want to demonstrate a helpful way to visualize the calculation.
As before, divide the scatterplot into quadrants (whose axes intersect at the mean of each variable, in this case 0). Now, for each point (i.e., for each pair of variables) find how far it is away from the x-axis and the y-axis.
data<-data.frame(scale(data))
knitr::kable(round(data,3),align='cc')| X | Y |
|---|---|
| -1.461 | -1.461 |
| -1.095 | -1.095 |
| -0.730 | -0.730 |
| -0.365 | -0.365 |
| 0.000 | 0.000 |
| 0.365 | 0.365 |
| 0.730 | 0.730 |
| 1.095 | 1.095 |
| 1.461 | 1.461 |
p<-ggplot(data,aes(X,Y))+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-2.5,2.5))+scale_y_continuous(limits = c(-2.5,2.5))+xlab("Zx")+ylab("Zy")
p+geom_segment(aes(x=data[9,1],xend=data[9,1],y=0,yend=data[9,2]),lty=3)+geom_segment(aes(x=0,xend=data[9,1],y=data[9,2],yend=data[9,2]),lty=3)+xlab("Zx")+ylab("Zy")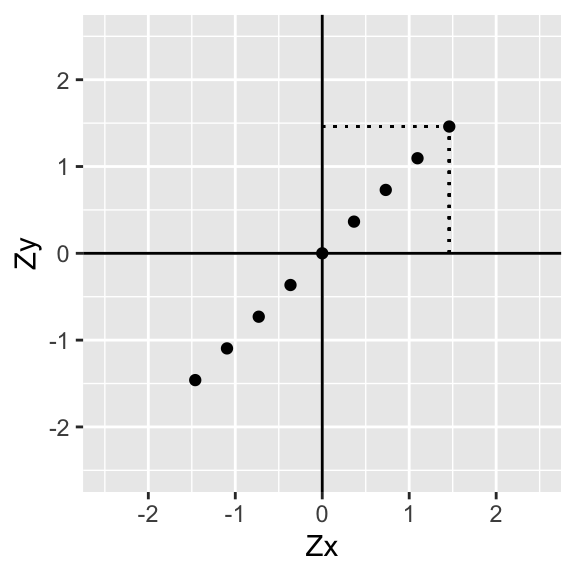
p+geom_segment(aes(x=data[9,1],xend=data[9,1],y=0,yend=data[9,2]),lty=3)+geom_segment(aes(x=0,xend=data[9,1],y=data[9,2],yend=data[9,2]),lty=3)+annotate("text", x = data[9,1], y=data[9,2], label = paste("(",round(data[9,1],2),",",round(data[9,2],2),")",sep=""),hjust=0,vjust=0,size=3)+xlab("Zx")+ylab("Zy")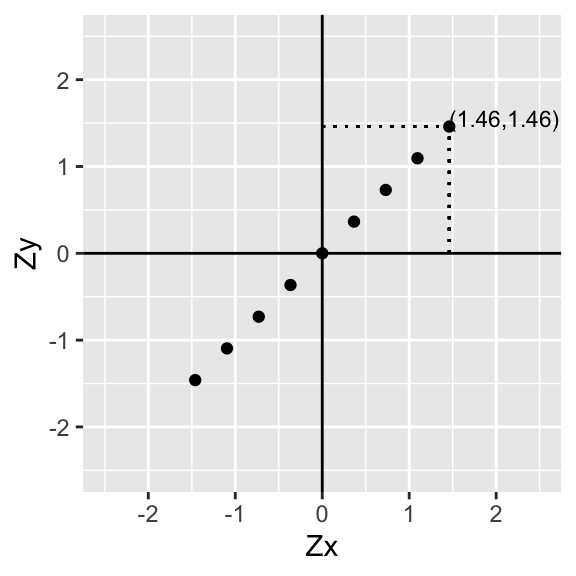
Now let’s go ahead and do this for every point:
p+geom_text(aes(label=paste("(",round(data$X,2),",",round(data$Y,2),")",sep=""),hjust=0, vjust=0),size=3)+xlab("Zx")+ylab("Zy")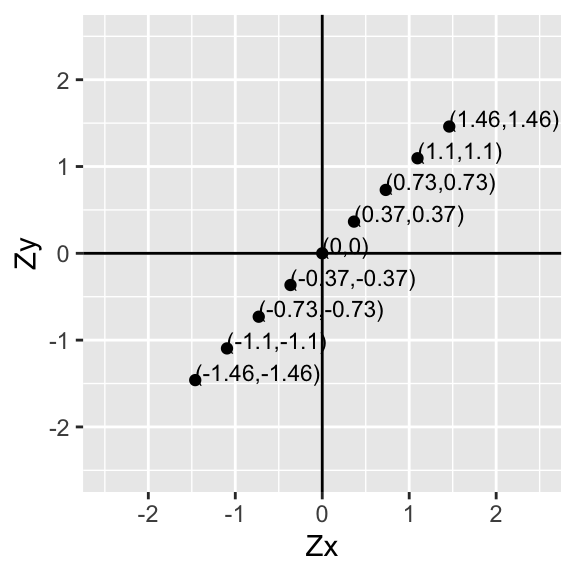
Since the mean of Zx is ˉx=0 and the mean of Zy is ˉy=0, for each point (xi,yi) we just found the deviations of each value from the mean (xi−ˉx,yi−ˉy)!
Now then, for each pair of values, multiply the two numbers together. Notice that this is the deviation of xi from its mean times the deviation of yi from its mean for all of the i pairs in our sample.
p+geom_text(aes(label=paste("(",round(data$X*data$Y,2),")",sep=""),hjust=0, vjust=0),size=3)+xlab("Zx")+ylab("Zy")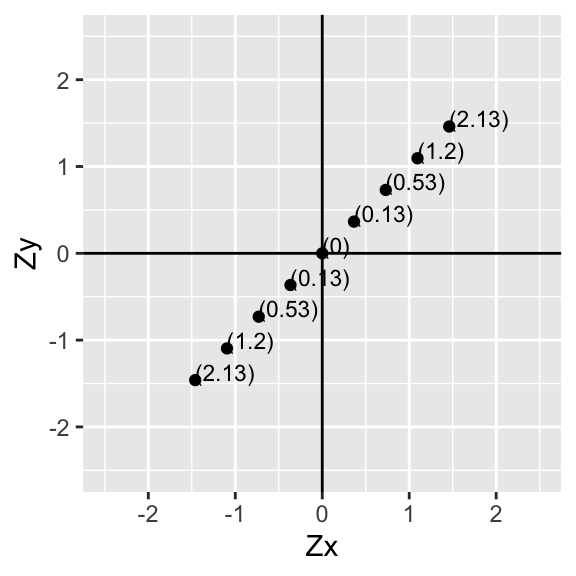
Let’s add them up in each quadrant and put the total in the middle:
p1<-ggplot(data,aes(X,Y))+geom_abline(slope = 1,intercept=0,color='gray50',lty=2)+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("Zy")+annotate("text",2,2,label=round(sum(data[data$X>0 & data$Y>0,]$X*data[data$X>0 & data$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data[data$X<0 & data$Y<0,]$X*data[data$X<0 & data$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data[data$X<0 & data$Y>0,]$X*data[data$X<0 & data$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data[data$X>0 & data$Y<0,]$X*data[data$X>0 & data$Y<0,]$Y),2))+xlab("Zx")+ylab("Zy")+geom_rug(color="gray50")
p1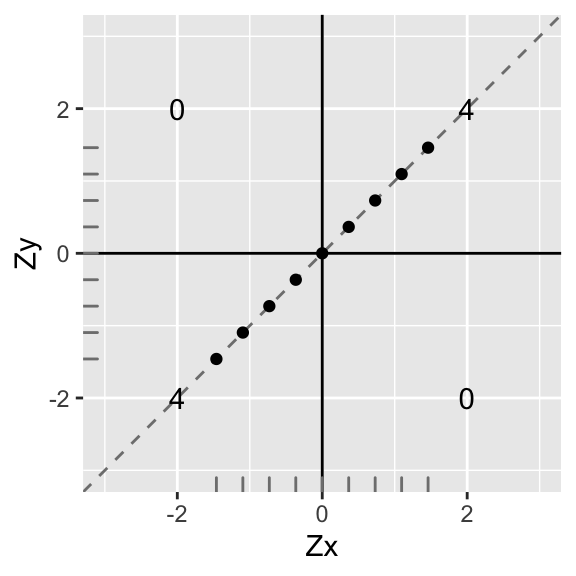
Now let’s use these totals to calculate the correlation coefficient: add up the total in each quadrant and divide by n−1.
∑ZxZyn−1=4+4+0+08=1
Perfect correlation (r=1)! Also, notice that the slope of the (dashed) line that the points lie on is also exactly 1…
What if the relationship were flipped?
data1<-data
data1$X<-data$X*-1
ggplot(data1,aes(X,Y))+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("Zy")+annotate("text",2,2,label=round(sum(data1[data1$X>0 & data1$Y>0,]$X*data1[data1$X>0 & data1$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data1[data1$X<0 & data1$Y<0,]$X*data1[data1$X<0 & data1$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data1[data1$X<0 & data1$Y>0,]$X*data1[data1$X<0 & data1$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data1[data1$X>0 & data1$Y<0,]$X*data1[data1$X>0 & data1$Y<0,]$Y),2))+xlab("Zx")+ylab("Zy")+geom_rug(color="gray50")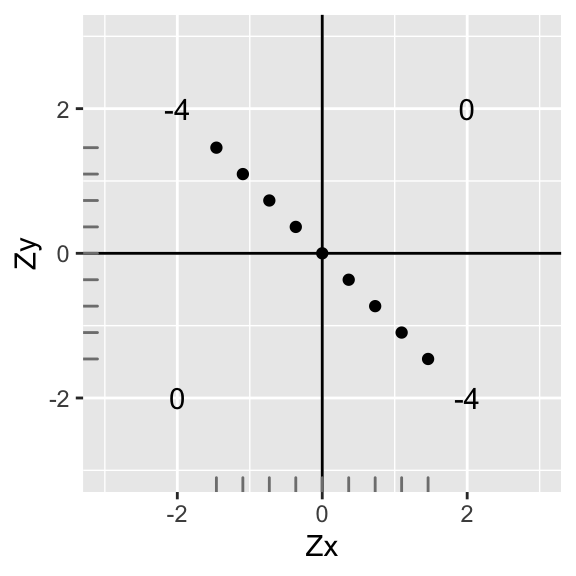
The sum of the deviations are the same, but the sign has changed. Thus, the correlation is the same strength, but different direction (r=-1) We have a perfect negative correlation: r=∑ZxZyn−1=−88=−1. Notice that the mean and standard deviation of x and y are still the same (we just rotated it 90o)
Now let’s see what would happen if data points were no longer perfectly linear. Let’s take the second data point from the bottom and scoot it up, making the y-value equal 0.
data1<-data
data1[2,2]<-0
ggplot(data1,aes(X,Y))+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("y")+annotate("text",2,2,label=round(sum(data1[data1$X>0 & data1$Y>0,]$X*data1[data1$X>0 & data1$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data1[data1$X<0 & data1$Y<0,]$X*data1[data1$X<0 & data1$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data1[data1$X<0 & data1$Y>0,]$X*data1[data1$X<0 & data1$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data1[data1$X>0 & data1$Y<0,]$X*data1[data1$X>0 & data1$Y<0,]$Y),2))+geom_rug(color="gray50")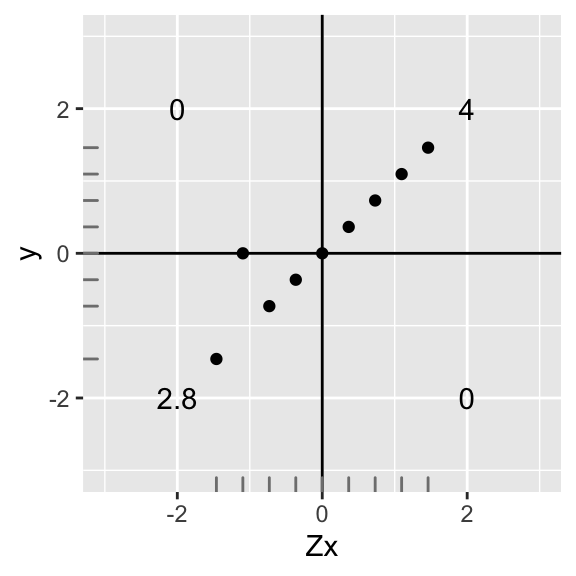
ggplot(data1,aes(X,Y))+geom_abline(slope = .92,intercept=0,color='gray50',lty=3)+
geom_abline(slope = 1,intercept=0,color='gray50',lty=2)+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("Zy")+annotate("text",2,2,label=round(sum(data1[data1$X>0 & data1$Y>0,]$X*data1[data1$X>0 & data1$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data1[data1$X<0 & data1$Y<0,]$X*data1[data1$X<0 & data1$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data1[data1$X<0 & data1$Y>0,]$X*data1[data1$X<0 & data1$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data1[data1$X>0 & data1$Y<0,]$X*data1[data1$X>0 & data1$Y<0,]$Y),2))+xlab("Zx")+ylab("Zy")+geom_rug(color="gray50")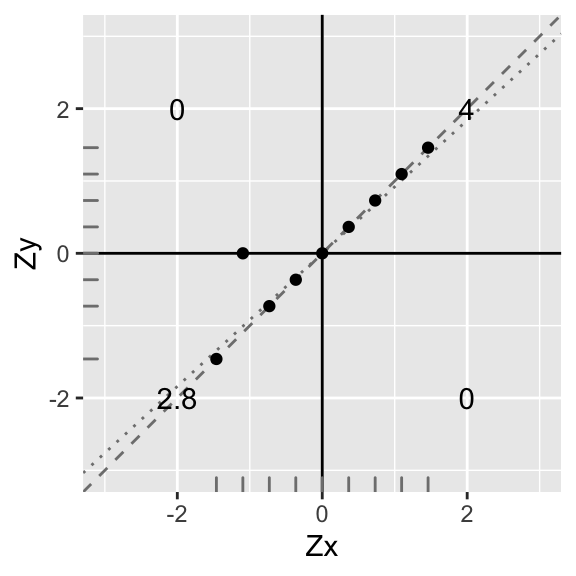
Uh oh, but since we changed a y-value, the mean of the ys no longer equals 1, and the standard deviation no longer equals 0. They are now My=.12 and SDy=.91; however, X still remains standardized because nothing changed (see distribution along the bottom).
If we ignore this fact and try to calculate the “correlation” we get: rfake=∑ZxYn−1=6.88=.85. However, if we go to the data and calculate the actual correlation, we get this:
knitr::kable(round(data1,3),align='cc')| X | Y |
|---|---|
| -1.461 | -1.461 |
| -1.095 | 0.000 |
| -0.730 | -0.730 |
| -0.365 | -0.365 |
| 0.000 | 0.000 |
| 0.365 | 0.365 |
| 0.730 | 0.730 |
| 1.095 | 1.095 |
| 1.461 | 1.461 |
print(paste("Correlation of X and Y: ",with(data1,cor(X,Y))))## [1] "Correlation of X and Y: 0.931128347758783"So the actual r=.93. Moving one data point up reduced our actual correlation from 1 to .93. But what is the relationship between the “fake” correlation we got by not standardizing Y (rfake=.85), and the actual correlation (.93)?
rfake=r×x.85=.93xx=.93.85=.91=sdY
Our “fake” correlation is just the covariance of X and Y! Remember, r=cov(X,Y)sdXsdY
Let’s standardize Y again and proceed:
data1$Y<-scale(data1$Y)
ggplot(data1,aes(X,Y))+geom_abline(slope = .9311,intercept=0,color='gray50',lty=3)+
geom_abline(slope = 1,intercept=0,color='gray50',lty=2)+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("Zy")+annotate("text",2,2,label=round(sum(data1[data1$X>0 & data1$Y>0,]$X*data1[data1$X>0 & data1$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data1[data1$X<0 & data1$Y<0,]$X*data1[data1$X<0 & data1$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data1[data1$X<0 & data1$Y>0,]$X*data1[data1$X<0 & data1$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data1[data1$X>0 & data1$Y<0,]$X*data1[data1$X>0 & data1$Y<0,]$Y),2))+xlab("Zx")+ylab("Zy")+geom_rug(color="gray50")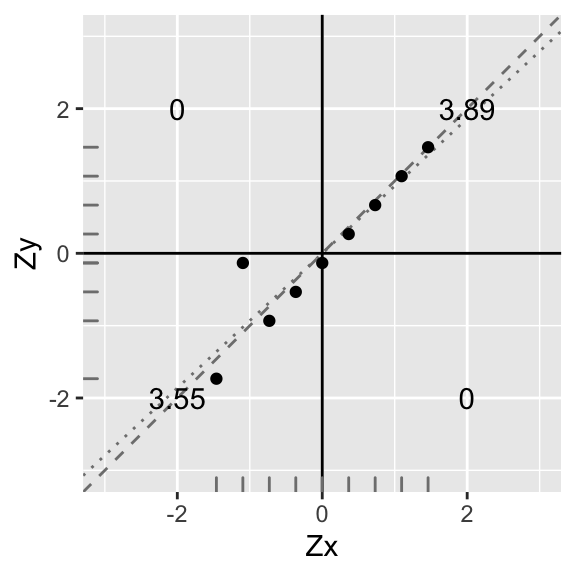
Again, you can see that the best-fitting line (dotted) has a slope somewhat less steep than before (compare to dashed line). Indeed, the slope is now r∑ZxZyn−1=3.55+3.898=7.448=0.93. Because the y-intercept is zero, the equation for the dotted line is Zy=.93×Zx. This will always be the case: Wen we have standardized variables, the slope of the line of best fit is equal to the correlation coefficient r.
OK, so what happens if our data are not linear? (We will go ahead and standardize our variables to avoid issues this time.)
data1<-data
data1$Y<--(data$Y^2)+1
data1<-data.frame(scale(data1))
ggplot(data1,aes(X,Y))+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("Zy")+annotate("text",2,2,label=round(sum(data1[data1$X>0 & data1$Y>0,]$X*data1[data1$X>0 & data1$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data1[data1$X<0 & data1$Y<0,]$X*data1[data1$X<0 & data1$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data1[data1$X<0 & data1$Y>0,]$X*data1[data1$X<0 & data1$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data1[data1$X>0 & data1$Y<0,]$X*data1[data1$X>0 & data1$Y<0,]$Y),2))+xlab("Zx")+ylab("Zy")+geom_rug(color="gray50")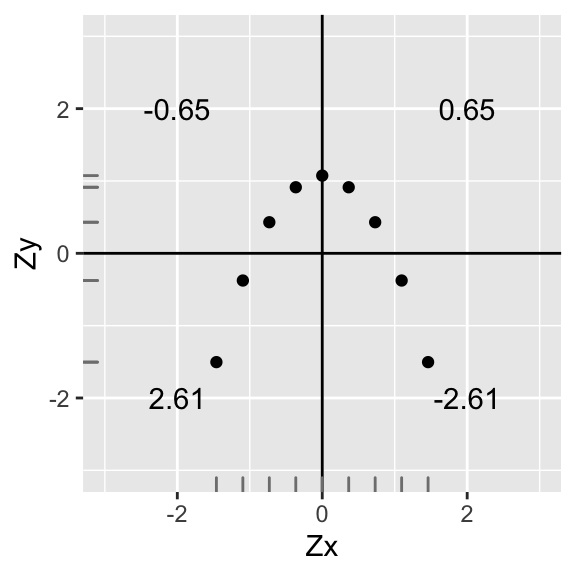
#mean(data1$Y)
#sd(data1$Y)We have r=∑ZxZyn−1=.65+(−.65)+2.61+(−2.61)8=08=0, zero correlation! This is because every point in a positive quadrant is cancelled out by a point in a negative quadrant!
However, there is still clearly a relationship between Zy and Zx! (Specifically, Zy=−Zx2+1). So calculating the correlation coefficient is only appropriate when you are interested in a linear relationship. As we will see, the same applies to linear regression.
Finally, let’s see what more realistic data might look like:
library(ggplot2)
library(MASS)
samples = 9
r = 0.5
data1 = as.data.frame(mvrnorm(n=samples, mu=c(0, 0), Sigma=matrix(c(1, r, r, 1), nrow=2), empirical=TRUE))
names(data1)<-c("X","Y")
ggplot(data1,aes(X,Y))+geom_point()+geom_hline(yintercept=0)+geom_vline(xintercept=0)+scale_x_continuous(limits=c(-3,3))+scale_y_continuous(limits = c(-3,3))+xlab("Zx")+ylab("Zy")+annotate("text",2,2,label=round(sum(data1[data1$X>0 & data1$Y>0,]$X*data1[data1$X>0 & data1$Y>0,]$Y),2))+
annotate("text",-2,-2,label=round(sum(data1[data1$X<0 & data1$Y<0,]$X*data1[data1$X<0 & data1$Y<0,]$Y),2))+
annotate("text",-2,2,label=round(sum(data1[data1$X<0 & data1$Y>0,]$X*data1[data1$X<0 & data1$Y>0,]$Y),2))+
annotate("text",2,-2,label=round(sum(data1[data1$X>0 & data1$Y<0,]$X*data1[data1$X>0 & data1$Y<0,]$Y),2))+xlab("Zx")+ylab("Zy")+geom_rug(color="gray50")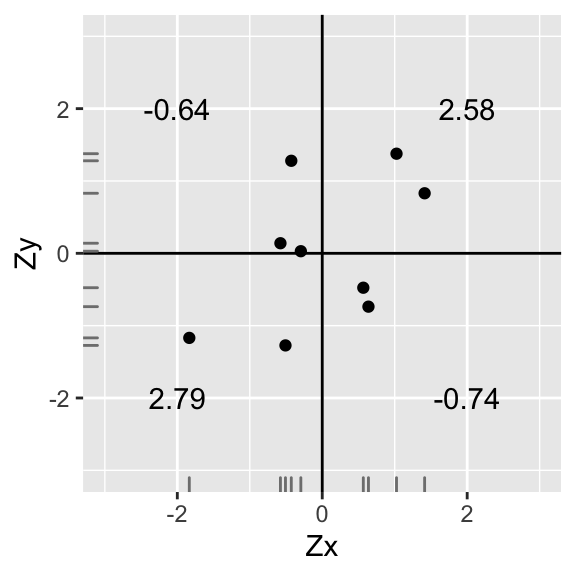
Here, we find that r=∑ZxZyn−1=(−0.18)+3.1+(−1.01)+2.098=48=0.5
A positive correlation, but not nearly as strong as before.
To recap,
r = strength of linear relationship between two variables
for variables x and y, measures how close points (x,y) are to a straight line
linear transformations (add/subtract a constant, multiply/divide by a constant) do not affect the value of r.
Now then, in the above case where the line fit perfectly (r=1), we could write our prediction for y (denoted ˆy) like so:
Zy=Zx⟶ˆy−ˉysdy=x−ˉxsdx
In this case, it was a perfect prediction! But when it is not perfect prediction, we need to calculate a slope coefficient for Zx
Regression
Correlation and regression are fundamental to modern statistics.
Regression techniques are useful when you want to model an outcome variable y as a function of (or in relationship to) predictor variables x1,x2,.... Specifically, regression is useful when you want
y=f(x1,x2,...)
Because this goal is so common, and because the tool is so general, regression models are ubiquitous in research today.
We are going to be talking here about situations where we model y as a linear function of x1,x2,...
y=b0+b1x1+b2x2+...+ϵ
We are interested in modeling the mean of our response variable y given some predictors x1,x2,.... Right now, think of regression as a function which gives us the expected value of y (ˆy) for a given value of x. The value ˆy is the predicted value, which will lie on the straight line that runs right through the middle of our scatterplot. Notice that some of the data will be above the predicted line and some will be below it: our ˆys will not perfectly match our y. The distances between the predicted (or “fitted”) values ˆy and the actual values y are called residuals (ϵ=y−ˆy). The residuals end up being very important conceptually: they represent the variability in y that is left after accounting for the best-fitting linear combination of your predictor(s) x (i.e., ˆy).
##Deriving regression coefficients!
Let’s keep it basic, because doing so will allow us to do something amazing using pretty basic math.
Let’s look at a special regression with one dependent variable y, one predictor x, and no intercept. Like we said above, the xs and ys we observed aren’t going to have a perfectly linear relationship: we need a residual term (ϵ) that capture deviations of our data from the predicted line ˆy=bx (“error”). Here’s the model:
y=bx+ϵˆy=bxsubtract bottom from top,y−ˆy=ϵ
Now, when we estimate b, our goal is to miminize the errors (the residuals ϵ=y−ˆy). Minimizing the errors/residuals will give us the best fitting line! But ϵi can be positive or negative, so we square them. Specifically, we want to choose b to minimize the sum of these squared residuals. Let’s do it! From above, we know that ϵ=y−bx, so ∑iϵ2i=∑i(yi−bxi)2. Let’s do a tiny bit of algebra (minb just means our goal is to find the value of b that minimizes the function:
minb∑iϵ2i=∑i(yi−ˆyi)2minb∑iϵ2i=∑i(yi−bxi)2=∑i(yi−bxi)(yi−bxi)=∑iy2i−2bxiyi+b2x2i
Recall that x and y are fixed. We want to know the value of b that will result in the smallest total squared error. We can find this value by taking the derivative of the error function (above) with respect to b: this results in a new function that tells you the slope of a line tangent to the original function for each value of b. Since the original function ∑i(yi−bxi)2 is a positive quadratic, we know that it has its minimum value at the bottom of the bend where the slope of the tangent line is zero. This is the minimum value of the error function! We just need to solve for b.
dropping subscripts for readabilityminb∑ϵ2=∑(y2−2bxy+b2x2)distribute sums, pull out constants, apply derivative operatorddb∑ϵ2=ddb∑y2−2b∑xy+b2∑x2=0−2∑xy+2b∑x2
set derivative equal to zero, solve for b−2∑xy+2b∑x2=02b∑x2=2∑xyb=∑xy∑x2
So the “least squares estimator” ˆb is ∑xy∑x2.
This means that our best prediction of ˆy given x is
ˆy=ˆbx=(∑ixiyi∑ix2i)x=∑iyixi∑ix2ix
So our prediction for y given x is a weighted average of all the observed yis.
This can be hard to see, so let’s say we observe the following data: y={−1,0,1},x={−1,1,0} Then given that x=1, our estimate ˆy is ∑iyixi∑ix2ix=−1−121+0121+1021=.5+0+0=.5
ggplot(data.frame(x=c(-1,1,0),y=c(-1,0,1)),aes(x,y))+geom_point()+geom_smooth(method=lm, se=F)+annotate(geom="point",x=1,y=.5,color="red")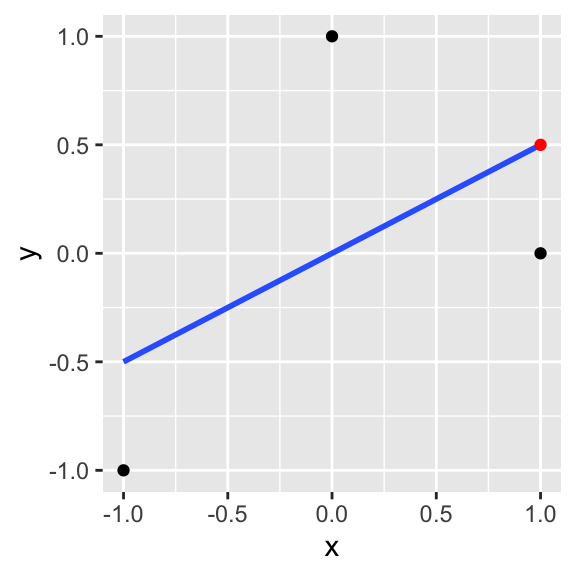
Look again at ˆb=∑xy∑x2 for a moment. The top part of the estimator looks kind of like covariance, and the bottom looks kind of like a variance. Indeed,
cov(X,Y)var(X)=∑(xi−ˉx)(yi−ˉy)/n−1∑(xi−ˉx)2/n−1=∑(xi−ˉx)(yi−ˉy)∑(xi−ˉx)2
The only difference is that cov(X,Y)var(X) scales the variables first, by subtracting the mean from each! Remember that in our simplified equation yi=bxi+ϵi, we are implicitly assuming that the y-intercept is zero (as it is when both variables are standardized). When it is, you are fine to use ˆb=∑xiyi∑x2i However, when you do have a y-intercept you want to find (which is usually the case), then the best estimator of the true slope b1 is ˆb1=cov(X,Y)var(X)=∑(xi−ˉx)(yi−ˉy)∑(xi−ˉx)2. Let me show you the difference with some play data.
x1<-1:20
y1<-rnorm(20)+.5*x1+5
data<-data.frame(x1,y1)
b_noint=sum(x1*y1)/sum(x1^2)
b_int=cov(x1,y1)/var(x1)
ggplot(data,aes(x1,y1))+geom_point()+scale_x_continuous(limits=c(0,20))+scale_y_continuous(limits=c(0,15))+geom_abline(slope=b_noint,intercept=0)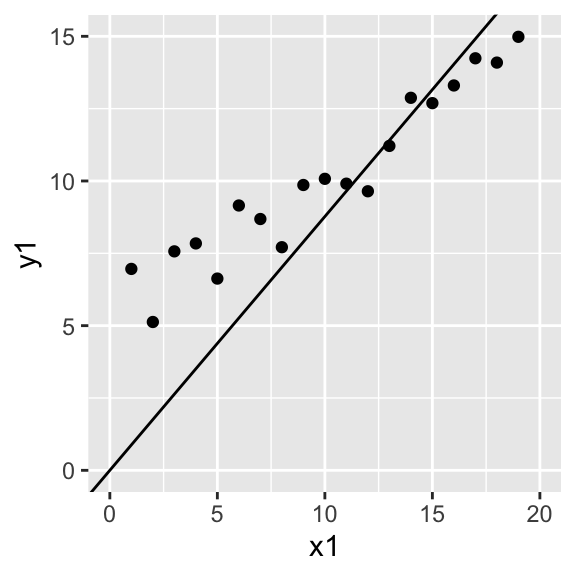
y2<-scale(y1)
x2<-scale(x1)
ggplot(data,aes(x2,y2))+geom_point()+geom_abline(slope=b_noint,intercept=0)
I wanted to show a derivation in the simplest case, but it works just as well with more variables. Here is a run-through of the same, but with vectors and matricies. let y=Xb+e where y is a vector, X is a matrix of all predictors, b is a vector of parameters to be estimated, and e is a vector of errors.
[y1y2⋮]=[x1,1x1,2x2,1x2,2⋮⋮][b1b2⋮]+[ϵ1ϵ2⋮]
e′e=(y−Xb)′(y−Xb)e′e=y′y−2b′X′y+b′X′Xbddbe′e=−2Xy+2b′X′Xset equal to zero and solve for b0=−2X′y+2b′X′X2X′y=2b′X′Xb=(X′X)−1X′y
Even if you are relatively unfamiliar with matrix algebra, you can see the resemblance that (X′X)−1X′y bears to 1∑x2∑xy.
###Testing (X′X)−1X′Y on some data
Let’s say our data are Y=10,13,14 and X=2,5,12. Let’s derive the regression coefficient estimates ˆb=b0,b1 using the estimator X′X−1X′y
yxx=xxxxxxXbxxx+xxe[101314]=[1215112][b0b1]+[ϵ1ϵ2ϵ3]
Now ˆb=(X′X)−1X′Y, so... Click button to expand the calculation:
So we found that the intercept estimate is 10.09 and the slope estimate is 0.35. Let’s check this result by conducting a regression on the same data:
lm(c(10,13,14)~c(2,5,12))##
## Call:
## lm(formula = c(10, 13, 14) ~ c(2, 5, 12))
##
## Coefficients:
## (Intercept) c(2, 5, 12)
## 10.0886 0.3544dat<-data.frame(x=c(2,5,12),y=c(10,13,14))
lm_eqn <- function(df){
m <- lm(y ~ x, df);
eq <- substitute(hat(italic(y)) == a + b %.% italic(x),
list(a = format(coef(m)[1], digits = 2),
b = format(coef(m)[2], digits = 2)))
as.character(as.expression(eq));
}
ggplot(dat,aes(x,y))+geom_point()+geom_smooth(method=lm,se=F)+geom_text(x = 5, y = 14, label = lm_eqn(dat), parse = TRUE)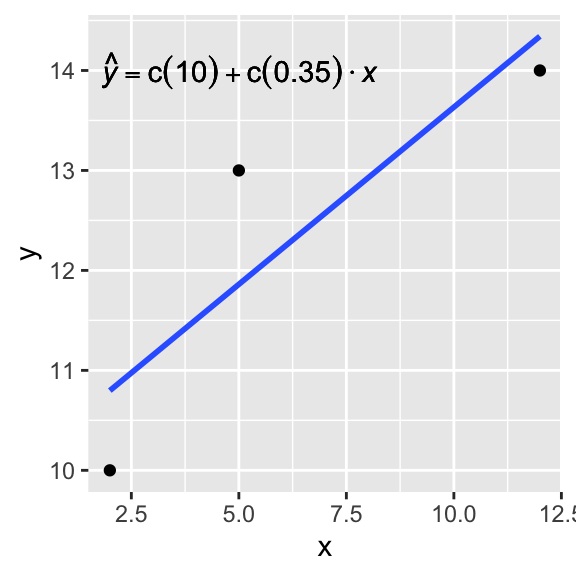
Why normally distributed errors?
Notice that we have derived regression coefficient estimates without making any assumptions about how the errors are distributed. But wait, you may say, if you already know something about regression: one assumption of regression (which is required for statistical inference) is that the errors are independent and normally distributed! That is,
yi=b0+b1xi+ϵi,xxxxxϵi∼N(0,σ2)
What does this say? Imagine there is a true linear relationship between x and y in the real world that actually takes the form y=b0+b1x. When we estimate ˆb0 and ˆb1, we are estimating these true population coefficients, but we are doing so impercisely based on observed data. The data we collect is always noisy and imperfect, and in statistics, we handle these imperfections by modeling them as random processes. Thus, for now we assume that the deviations of y from our predicted ˆy are random and follow a normal distribution. Equivalently, we can say that for a given xi, yi is normally distributed, with a mean of ˆyi and a standard deviation of σ2.
Let’s visualize this function and use it to create some data, add some noise to it, and run a regression to see if we can estimate the true parameters. But what are those parameters going to be? How about b0=1 and b1=2, so we have yi=1+2xi+ϵi. Our predicted values of y (ˆy) are just ˆy=2xi.
x<-seq(-5,4.99,.01)
y<-1+2*x
qplot(x,y)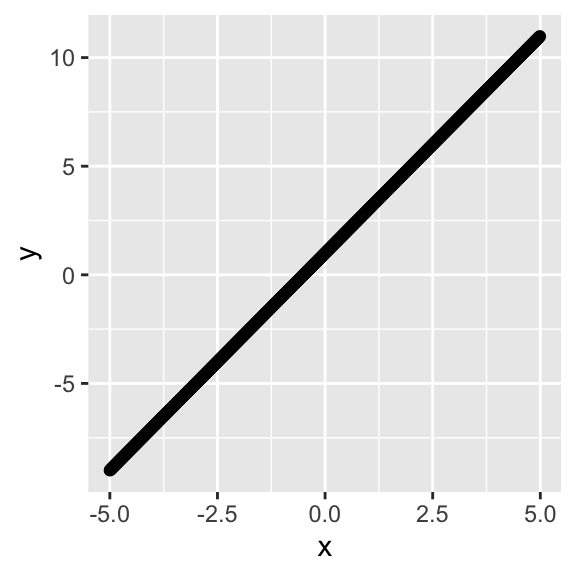
#ggplot()+geom_abline(slope=2,intercept=1)+
# scale_y_continuous(limits=c(-4,4))+scale_x_continuous(limits=c(-4,4))Now let’s give a little random error to each estimate by adding a draw from a standard normal distribution, ϵi∼N(μ=0,σ2=1).
#x<-seq(-4,4,.1)
y<-y+rnorm(1000,mean=0,sd=1)
qplot(x,y)#+geom_abline(slope=2,intercept=1,color="gray50")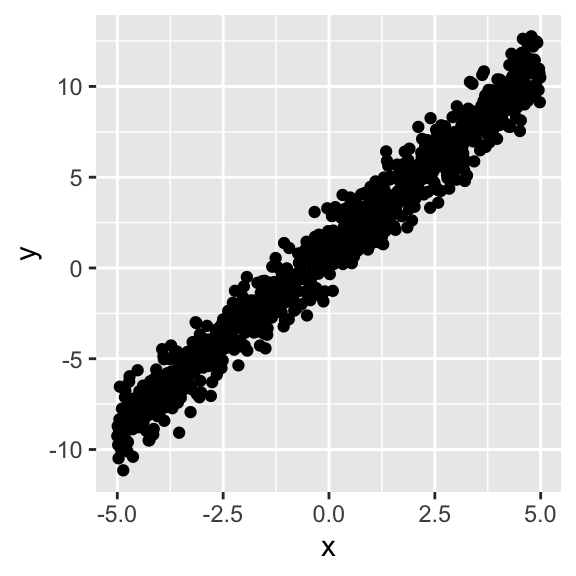
# scale_y_continuous(limits=c(-4,4))+scale_x_continuous(limits=c(-4,4))Since we set the standard deviation of the errors equal to one (i.e., σ=1), ~95% of the observations will lie within 2σ of the predicted values ˆy.
Now let’s estimate the best-fitting line, given only a sample of x and y (say, n=50 from the population). We will plot it (gray) along with the line we know to be true, namely y=1+2x (white).
dat<-data.frame(x,y)
dat0<-data.frame(x,y)
sum1<-summary(lm(data=dat[sample(nrow(dat),size = 50,replace = F),],y~x))
sum1##
## Call:
## lm(formula = y ~ x, data = dat[sample(nrow(dat), size = 50, replace = F),
## ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.9826 -0.6407 0.1432 0.5365 2.1388
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.13011 0.12946 8.729 1.78e-11 ***
## x 1.96966 0.04761 41.368 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9149 on 48 degrees of freedom
## Multiple R-squared: 0.9727, Adjusted R-squared: 0.9721
## F-statistic: 1711 on 1 and 48 DF, p-value: < 2.2e-16beta<-coef(sum1)[1:2,1]
qplot(x,y)+geom_abline(intercept=1,slope=2,color="white")+geom_abline(intercept=beta[1],slope=beta[2],color="gray50")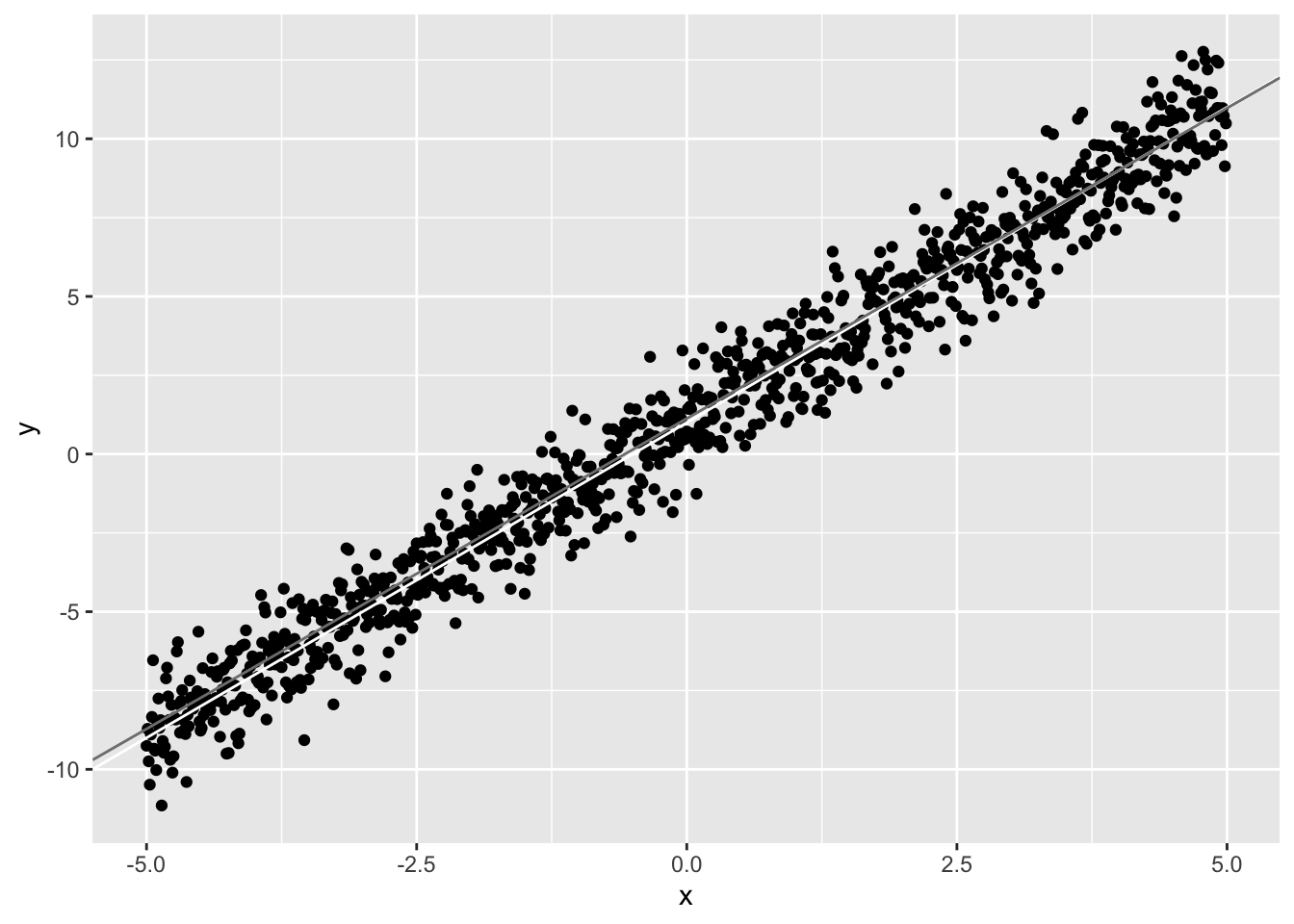 We generated the data to have ϵ∼N(μ=0,σ2=1). Notice that the coefficient estimate for x, (ˆb1= 1.97) is very close to the actual value (b1=2), and the coefficient estimate for the intercept (ˆb0= 1.13) is close to it’s actual value (b0=1). Notice also that the residual standard error is also close to 1. This is the standard deviation of the residuals (ϵ=y−ˆy) and thus it is an estimate of σ above.
We generated the data to have ϵ∼N(μ=0,σ2=1). Notice that the coefficient estimate for x, (ˆb1= 1.97) is very close to the actual value (b1=2), and the coefficient estimate for the intercept (ˆb0= 1.13) is close to it’s actual value (b0=1). Notice also that the residual standard error is also close to 1. This is the standard deviation of the residuals (ϵ=y−ˆy) and thus it is an estimate of σ above.
If we repeat this 1000 times (i.e., based on new random samples of 50), we get 1000 different estimates of the slope ˆb1
#betas<-NULL
#sigma2<-NULL
betas<-vector()
sigma2<-vector()
for(i in 1:1000){
sum1<-summary(lm(data=dat[sample(nrow(dat),size = 50,replace = F),],y~x))
sum1
betas<-rbind(betas,coef(sum1)[1:2,1])
sigma2<-rbind(sigma2,sum1$sigma^2)
}
qplot(x,y)+geom_abline(intercept=betas[,1],slope=betas[,2],color="gray50")+geom_abline(intercept=1,slope=2,color="white")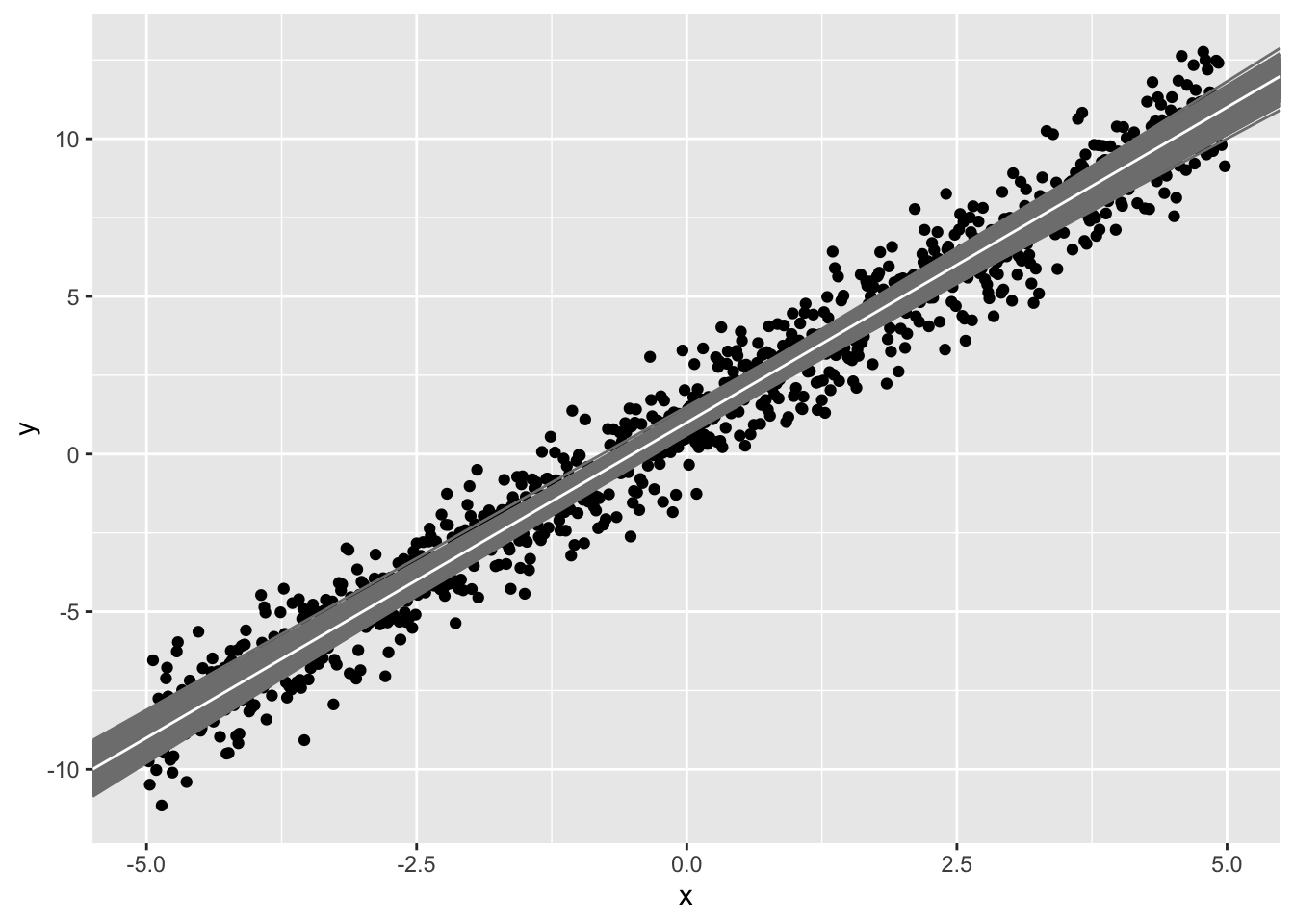
sample1<-data.frame(x,y)[sample(1:1000,size=50),]
#ggplot(sample1,aes(x,y))+geom_point()+geom_smooth(method='lm',se = T,level=.9999,color='gray50')
#ggplot(sample1,aes(x,y))+geom_point()+geom_abline(intercept=betas[,1],slope=betas[,2],color="gray50")+geom_abline(intercept=1,slope=2,color="white")Each sample (i.e, your observed data) has error. Thus, each linear model also has error (in the intercept and in the slope). Notice that the prediced values for each sample (gray lines) tend to be better closer to the point (ˉx,ˉy) and worse (farther from the white line) at the extremes.
When taking 1000 samples of 50 data points from our population, the estimates we get for the intercept and slope (i.e., ˆb0 and ˆb1) range from and from respectively.
As we saw above, we can also estimate σ2 from the sample variance of the residuals for each regression (∑(yi−ˆy)2n−2). (We divide by n−2 here because ˆy requires estimating both beta parameters, which uses up 2 degrees of freedom.) Let’s plot the distribution of these estimates:
library(tidyr)
ests<-betas
colnames(ests)<-c("Est Intercept", "Est Slope")
colnames(sigma2)<-"Est Var"
ests<-gather(data.frame(ests,sigma2))
ggplot(ests,aes(x=value))+geom_histogram(bins=30)+facet_grid(~key,scales="free_x")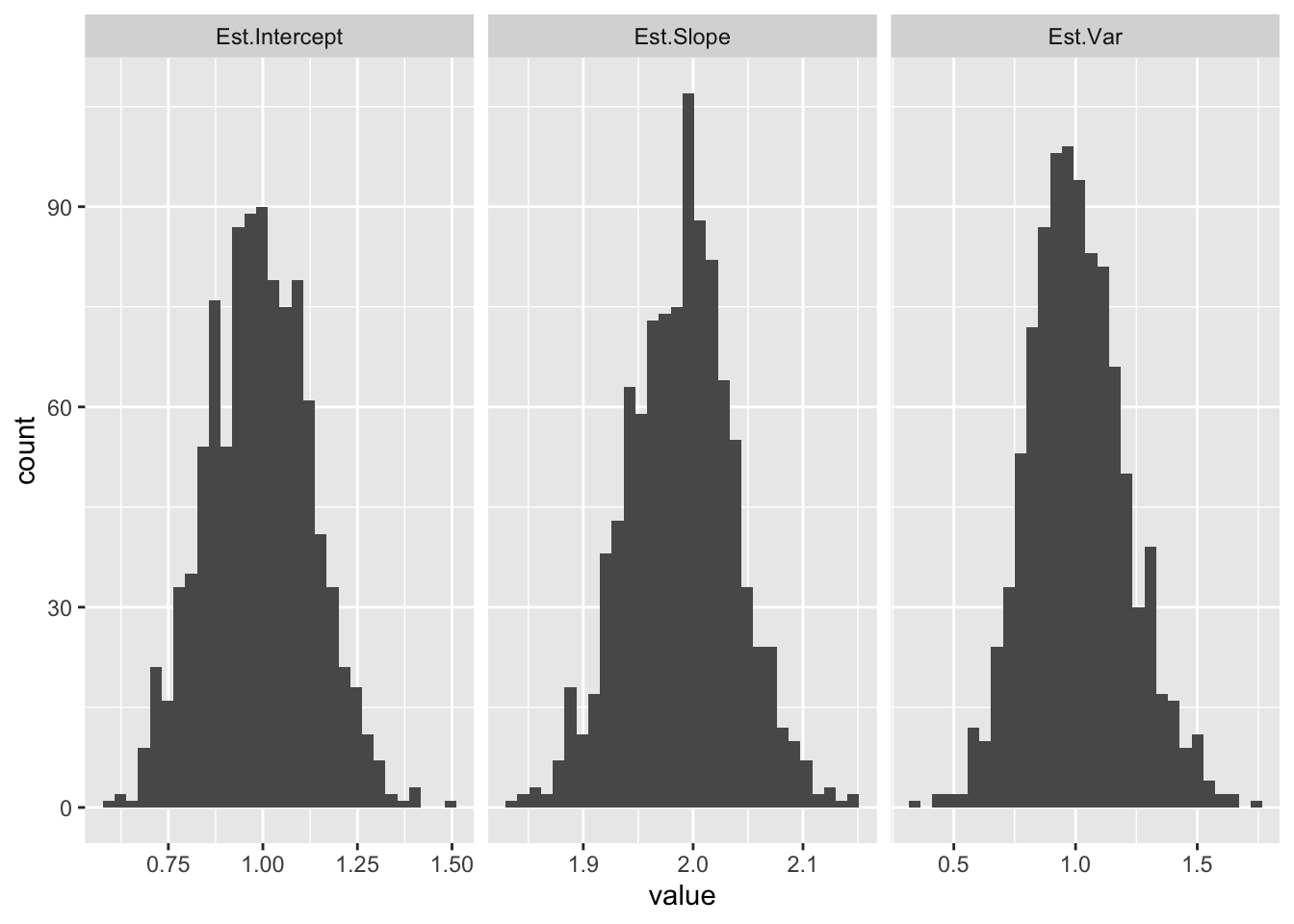
Notice how the mean of each distribution is equal to the population value (b0=1,b1=2,σ=1).
Normal-errors assumption and homoskedasticity
But let’s not get ahead of ourselves! Back to this for a moment:
yi=b0+b1xi+ϵi,xxxxxϵi∼N(0,σ2)
For a given yi, b0, b1, and xi, the quantity b0+b1xi gets added to the ϵi∼N(0,σ2), thus shifting the mean from 0, but leaving the variance alone. Thus, we can write
yi∼N(b0+b1xi,σ2)
This means that we are modeling y as a random variable that is normally distributed, with a mean that depends on x. Thus, given x, y has a distribution with a mean of b0+b1x and a standard deviation of σ. Our predicted value ˆy is the conditional mean of yi given x.
We can see this below. For a given (range of) x, the y should be normally distributed, N(μ=b0+b1x,σ2=1). We plot the observed density (red) and the theoretical density (blue).
Plot of density of y given x; plot includes entire “population” of 1000:
dat<-data.frame(x,y)
breaks <- seq(min(dat$x), max(dat$x), len=8)
dat$section <- cut(dat$x, breaks)
## Get the residuals
dat$res <- residuals(lm(y ~ x, data=dat))
## Compute densities for each section, and flip the axes, and add means of sections
## Note: the densities need to be scaled in relation to the section size (2000 here)
dens <- do.call(rbind, lapply(split(dat, dat$section), function(x) {
res <- data.frame(y=mean(x$y)+seq(-3,3,length.out=50),x=min(x$x) +2*dnorm(seq(-3,3,length.out=50)))
## Get some data for normal lines as well
xs <- seq(min(x$res)-2, max(x$res)+2, len=50)
res <- rbind(res, data.frame(y=xs + mean(x$y),
x=min(x$x) + 2*dnorm(xs, 0, sd(x$res))))
res$type <- rep(c("theoretical", "empirical"), each=50)
res
}))
dens$section <- rep(levels(dat$section), each=100)
## Plot both empirical and theoretical
ggplot(dat, aes(x, y)) +
geom_point() +
geom_smooth(method="lm", fill=NA, lwd=2) +
geom_path(data=dens, aes(x, y, group=interaction(section,type), color=type), lwd=1)+
theme_bw() + theme(legend.position="none")+
geom_vline(xintercept=breaks, lty=2)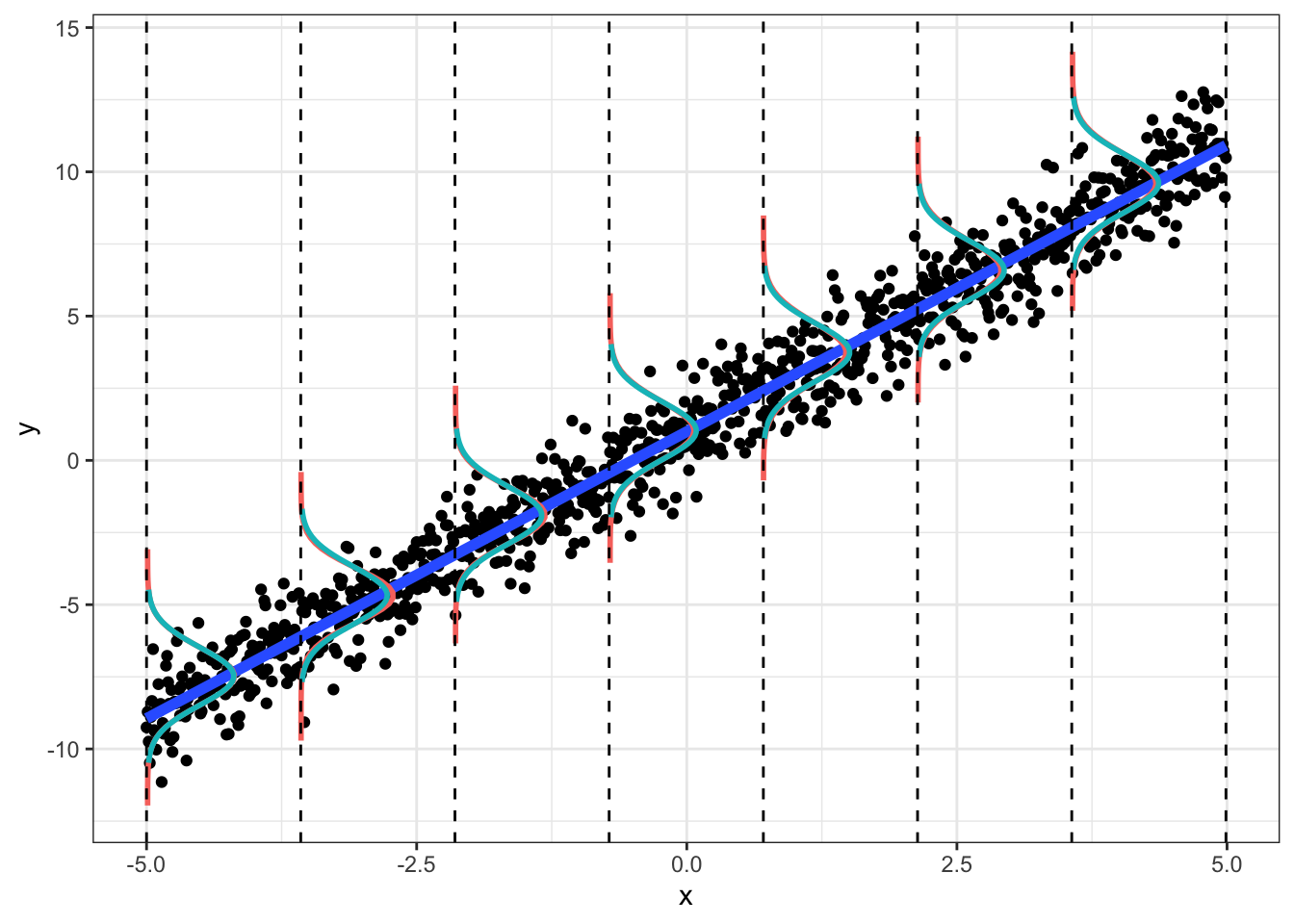
Plot of density of y given x for a sample of 50 data points:
dat<-data.frame(x,y)
dat<-dat[sample(size=50,nrow(dat),replace=F),]
breaks <- seq(min(dat$x), max(dat$x), len=8)
dat$section <- cut(dat$x, breaks)
## Get the residuals
dat$res <- residuals(lm(y ~ x, data=dat))
## Compute densities for each section, and flip the axes, and add means of sections
## Note: the densities need to be scaled in relation to the section size (2000 here)
dens <- do.call(rbind, lapply(split(dat, dat$section), function(x) {
res <- data.frame(y=mean(x$y)+seq(-3,3,length.out=50),x=min(x$x) +2*dnorm(seq(-3,3,length.out=50)))
## Get some data for normal lines as well
xs <- seq(min(x$res)-2, max(x$res)+2, len=50)
res <- rbind(res, data.frame(y=xs + mean(x$y),
x=min(x$x) + 2*dnorm(xs, 0, sd(x$res))))
res$type <- rep(c("theoretical", "empirical"), each=50)
res
}))
dens$section <- rep(levels(dat$section), each=100)
## Plot both empirical and theoretical
ggplot(dat, aes(x, y)) +
geom_point() +
geom_smooth(method="lm", fill=NA, lwd=2) +
geom_path(data=dens, aes(x, y, group=interaction(section,type), color=type), lwd=1)+
theme_bw() + theme(legend.position="none")+
geom_vline(xintercept=breaks, lty=2)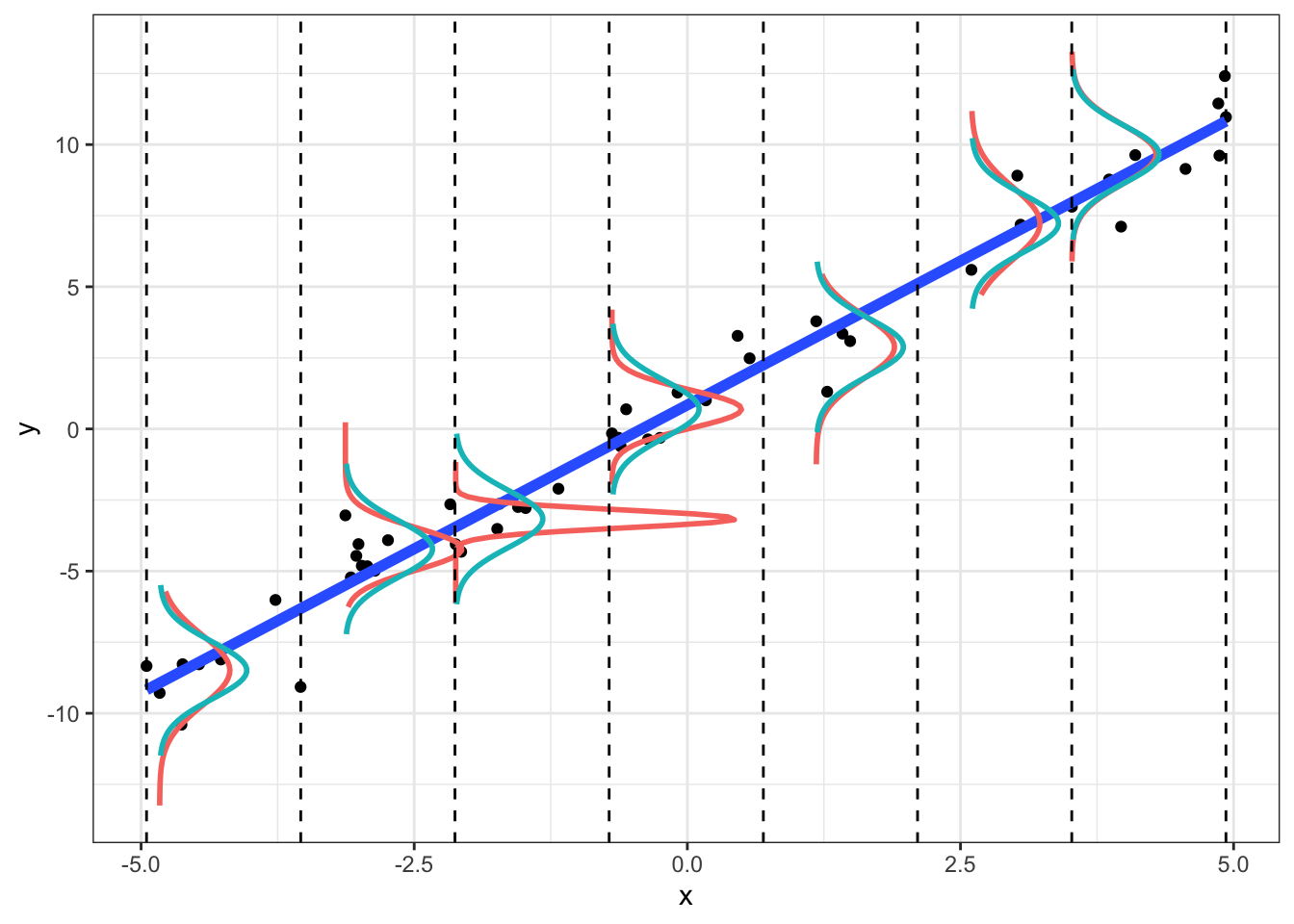
Notice that in the sample, the empirical densities are not exactly normal with constant variance (we wouldn’t expect them to be; this is just a small sample). However, we can example a plot of residuals vs. fitted-values (or vs. x) to see if the scatter looks random. We can also formally test for heteroskedasticity
samp.lm<-lm(data=dat,y~x)
dat$fvs<-samp.lm$fitted.values
dat$res<-samp.lm$residuals
ggplot(dat, aes(fvs,res))+geom_point()+geom_hline(yintercept=0)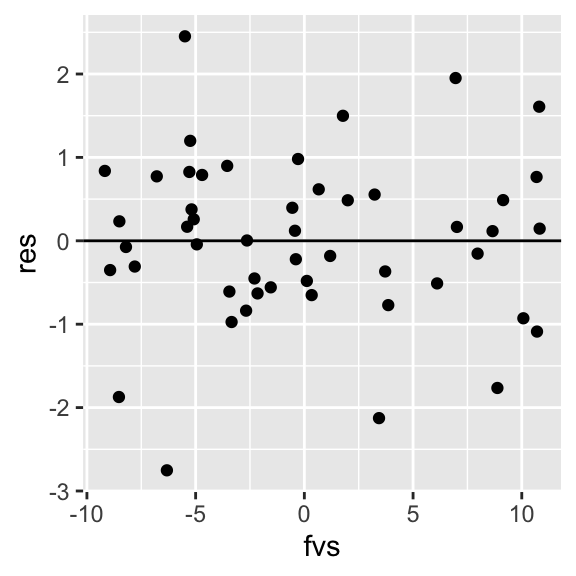
library(lmtest)
lmtest::bptest(samp.lm)##
## studentized Breusch-Pagan test
##
## data: samp.lm
## BP = 0.026574, df = 1, p-value = 0.8705In the Breusch-Pagan test, the null hypothesis is that variance is constant. Thus, if p<.05 we have reason to suspect that the heteroskedasticity assumption might be violated. Also, if our residual plot shows any thickening/widening, or really any observable pattern, this is another way of diagnosing issues with nonconstant variance.
To see if our residuals are normally distributed, we can compare quantiles of their distribution to expanded quantiles under a normal distribution. If we plot them against each-other, their match would be indicated by all points falling on a straight line (with deviations from the line indicating non-normality). There are also hypothesis tests, such as the Shapiro-Wilk test, that assess the extent of deviation from normality. Here again, the null hypothesis is that the observed distribution matches a normal distribution.
plot(samp.lm, which=c(2))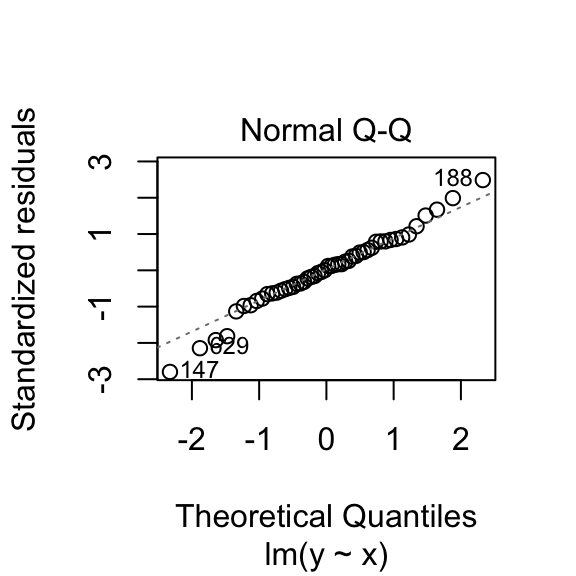
shapiro.test(dat$res)##
## Shapiro-Wilk normality test
##
## data: dat$res
## W = 0.9822, p-value = 0.6476This normal-errors assumption implies that at each x the scatter of y around the regression line is Normal. The equal-variances assumption implies that the variance of y is constant for all x (i.e., “homoskedasticity”). As we can see above (comparing empirical to theoretical distributions of y|x), they will never hold exactly for any finite sample, but we can test them.
##Sampling distributions of coefficient estimates
The normal-errors assumption allows us to construct normal-theory confidence intervals and to conduct hypothesis tests for each parameter estimate.
Because ˆb0 and ˆb1 are statistics, they have a sampling distribution! In fact, we have already seen them (above), when we repeatedly estimated the coefficients based on samples of 50.
We can get empirical 95% confidence intervals by finding the quantiles that cut off the bottom 2.5% and the top 2.5% of each distribution:
library(tidyr)
cutoff95<-apply(data.frame(betas,sigma2),2,function(x)quantile(x,probs=c(.025,.975)))
colnames(cutoff95)<-c("Est.Intercept","Est.Slope","Est.Var")
cutoff95## Est.Intercept Est.Slope Est.Var
## 2.5% 0.7187877 1.889069 0.6385057
## 97.5% 1.2616610 2.086461 1.4419042betas95<-data.frame(est.int=betas[!(is.na(cut(betas[,1],breaks=cutoff95[,1]))),1],est.slope=betas[!(is.na(cut(betas[,2],breaks=cutoff95[,2]))),2],est.sigma2=sigma2[!(is.na(cut(sigma2,breaks=cutoff95[,3])))])
cutoff95<-gather(data.frame(cutoff95))
ggplot(ests,aes(x=value))+geom_histogram(bins=30)+facet_grid(~key,scales="free_x")+geom_vline(data=cutoff95,aes(xintercept=value),color="red",lty=3)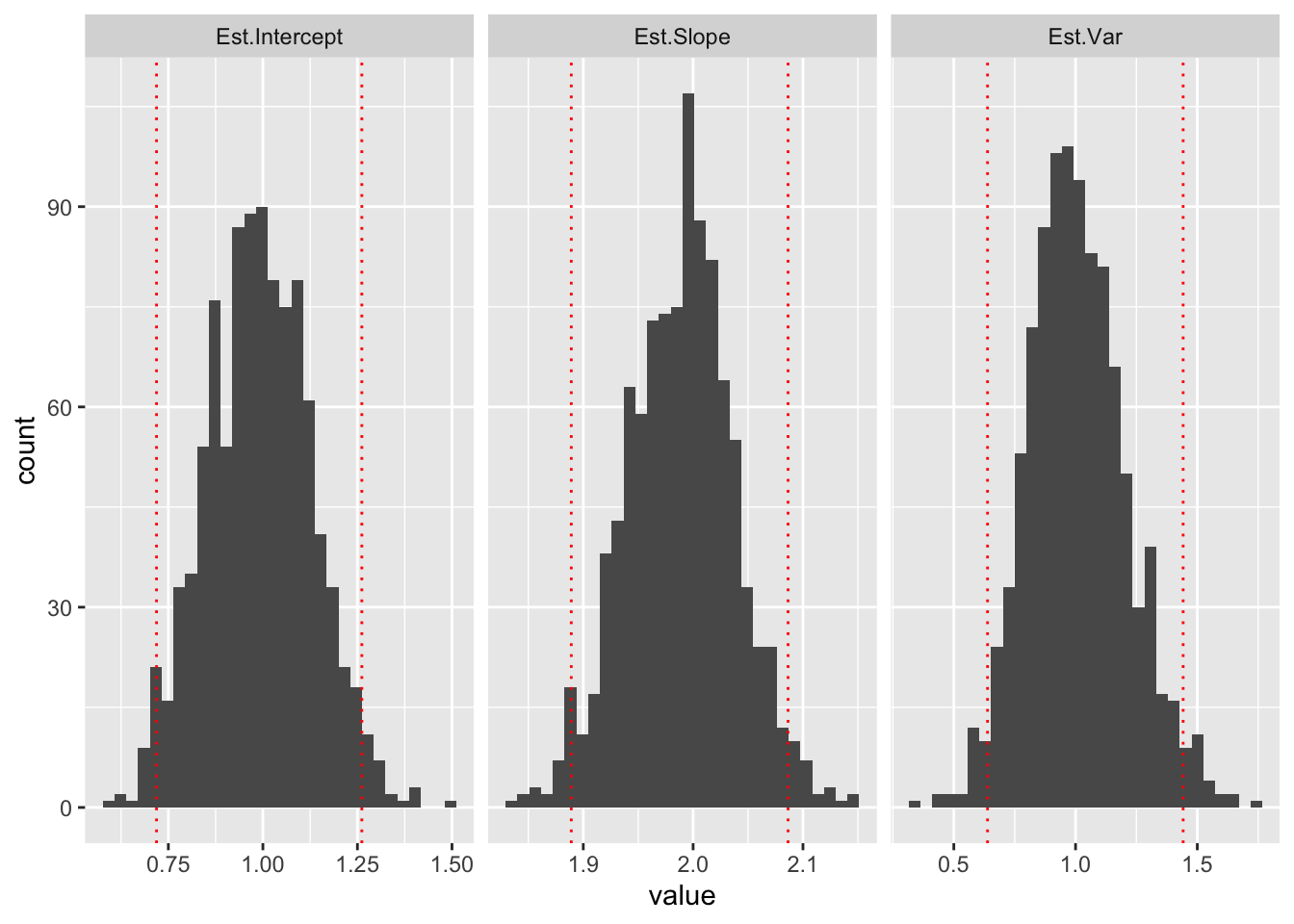
These are empirical confidence intervals (the middle 95% of the sampling distribution of each parameter).
But how can we get this from just a sample of the observed data?
We know that the (least squares) best estimate of b1 is ˆb1=∑(xi−ˉxi)(yi−ˉyi)∑(xi−ˉxi)2.
Because the regression line always passes through the point (ˉx,ˉy), we can plug those values in rearrange the equation to find that ˆb0=ˉy−ˆbˉx.
But what about the variance of these estimates? Let’s find it!
Var[ˆb1]=Var[∑(xi−ˉx)(yi−ˉy)∑(xi−ˉx)2]=Var[∑(xi−ˉx)∑(xi−ˉx)2yi]=Var[∑(xi−ˉx)∑(xi−ˉx)2(b0+b1xi+ϵi)]because only ϵi is a random variable, ϵ∼N(0,σ2),=∑(xi−ˉxi)2(∑(xi−ˉx)2)2Var[ϵi]=1∑(xi−ˉx)σ2
We could do something similar to find the variance of ˆb0, but in practice the intercept is much less interesting than the slope.
Typically, we are interested in whether changing x is associated with changes in y, which is the same as testing the null hypothesis that b1 is zero, or H0:b1=0
We also showed earlier that ˆb1=∑(xi−ˉx)∑(xi−ˉx)2yi. Thus, ˆb1 is a linear combination of the yis.
But wait! We know that yi∼N(b0+b1xi,σ2)
We also know that a linear combination of normally distributed variables is itself normally distributed! (Indeed, a linear combination of any independent random variable converges to a Normal distribution with as n→∞)
Since ˆb1 is a linear combination of the yis, ˆb1 is normally distributed as well.
This means ˆb1∼N(E[ˆb1],Var[ˆb1]).
We already found the variance of the distribution of ˆb1, Var[ˆb1]=σ2∑(xi−ˉx)2
We have already seen that E[ˆb1]=b1, but proving it isn’t too bad either:
E[ˆb1]=E[∑(xi−ˉx)∑(xi−ˉx)2yi]=E[∑(xi−ˉx)∑(xi−ˉx)2(b0+b1xi+ϵi)]=∑(xi−ˉx)∑(xi−ˉx)2E[b0+b1xi+ϵi]=∑(xi−ˉx)∑(xi−ˉx)2(b0+b1xi)=b0(∑(xi−ˉx)∑(xi−ˉx)2)+b1(∑(xi−ˉx)xi∑(xi−ˉx)2)=b0(0)+b1=(1)=b1
Thus, we can now say that ˆb1∼N(b1,σ2∑(xi−ˉx)2)
We don’t know σ2 but we do have an unbiased estimator of it: s2=∑(yi−ˆy)2n−2
In a previous post, we showed that for sample of size n from x∼N(μ,σ2), and a sample variance of s2=∑(x−ˉx)2n−1, then ˉx−μ√s2/n∼t(n−1)
Since ˆb1∼N(μ=b1,σ2/∑(x−ˉx)2), we have
ˆb1−b1√s2/∑(x−ˉx)2∼t(n−2)
We can check to see if this makes sense with our data above. Recall that we repeatedly sampled 50 data points (x,y), ran a regression, and found ˆb1. We thus created a sampling distribution of those values for n=50
b1<-ests[ests$key=="Est.Slope",]
ggplot(b1,aes(x=value))+geom_histogram(bins=30)+geom_text(aes(x=1.9, y=75),label=paste("mean=",round(value),2)))+ geom_text(aes(x=1.9, y=60),label=paste("sd=",round(sd(value),3)))
#mean(b1$value)
#sd(b1$value)## Error: <text>:2:112: unexpected ')'
## 1: b1<-ests[ests$key=="Est.Slope",]
## 2: ggplot(b1,aes(x=value))+geom_histogram(bins=30)+geom_text(aes(x=1.9, y=75),label=paste("mean=",round(value),2)))
## ^We know the true b1 is 2.0 and the variance is σ2/∑(x−ˉx)2. The sampling distribution (for samples of size 50) will converge to these values.
Notice that the estimate of the variance depends on the actual sample values. Interestingly, we get pretty close to the empirical value based on one sample of size 50:
x_samp=sample(x,size=50)
sqrt(1/sum((x_samp-mean(x_samp))^2))## [1] 0.0447268Pretend all we observe are 50 observations. We can construct normal theory confidence intervals and conduct t-tests of the null hypothesis that ˆb1 is zero. First we estimate ˆb1 and s2/∑(x−ˉx)2. This means we have to estimate s2=∑(yi−ˆyi)2n−2. Finally, we will conduct a t-test (df=n−2) and also construct a 95% CI for our estimate, ˆb1±t∗(α=.975, df=48)×s2∑(x−ˉx)2
Here are our coefficient estimates:
samp=dat[sample(nrow(dat),size = 50,replace = F),]
#coefficients
b1<-with(samp, sum((x-mean(x))*(y-mean(y)))/sum((x-mean(x))^2))
b0<-with(samp, mean(y)-b1*mean(x))
paste("b0:",round(b0,4))## [1] "b0: 0.8434"paste("b1:",round(b1,4))## [1] "b1: 2.0241"Here is our estimated variance s2:
#residuals
e<-samp$y-(b0+b1*samp$x)
#MSE
s2<-sum(e^2)/(50-2)
s2## [1] 1.008651Here is our standard error (standard deviation of the sampling distribution for ˆb1):
#standard deviation of the sampling distribution (standard error)
se_b1<-with(samp, sqrt(s2/sum((x-mean(x))^2)))
se_b1## [1] 0.04713645#for the slope too: see below
se_b0<-with(samp,sqrt(s2*((1/50)+(mean(x)^2/sum((x-mean(x))^2)))))Let’s combine these to form a 95% confidence interval. We will use a critical t∗(48)=2.0106 value that cuts off 2.5% in either tail.
#95% CI:
b1+c(qt(.025,48)*se_b1,qt(.975,48)*se_b1)## [1] 1.929284 2.118833Thus, there’s a 95% chance that the true b1 is captured by the interval [1.929, 2.119]
Equivalently, we could test the null hypothesis of no effect H0:b1=0 versus the alternative hypothesis HA:b1≠0:
First we find the test statistic and the p-value (below):
# t test (H0: b1=0)
t=(b1-0)/se_b1
t## [1] 42.9404# pvalue
2*(1-pt(t,df = 48))## [1] 0So t= 42.940405, p= 0. Let’s confirm with R.
#confirm with R
samp.lm<-lm(y~x, data=samp)
summary(samp.lm)##
## Call:
## lm(formula = y ~ x, data = samp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.75221 -0.54629 0.05986 0.60153 2.45200
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.84340 0.14343 5.88 3.82e-07 ***
## x 2.02406 0.04714 42.94 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.004 on 48 degrees of freedom
## Multiple R-squared: 0.9746, Adjusted R-squared: 0.9741
## F-statistic: 1844 on 1 and 48 DF, p-value: < 2.2e-16In much the same fashion, you can also construct 95% confidence intervals and conduct hypotheses tests for the intercept b0.
However, the standard deviation of the sampling distribution of b0 (i.e., the standard error) is different! We wont walk through the derivation, but it is very similar to that above for b1. You wind up with this for the variance:
Var[b0]=σ2(1n+ˉx2∑(xi−ˉx)2) Again, since can’t know σ2, we use the estimator s2=∑(yi−ˆy)2n−2 as before. Thus, the standard error of the sampling distribution of b0 is
s.e.(b0)=s√1n+ˉx2∑(xi−ˉx)2or,equivalentlys.e.(b0)=s√n√1+ˉx2∑(xi−ˉx)2/n I included the second formulation of the standard error so that you can see that it is a product of the standard error of a variable’s mean (i.e., s√n).
So a 95% confidence interval for b0 looks like
ˆb0±t∗(n−2)∗s.e.(b0) In our specific case, ˆb0 is 0.8434 and our standard error is 0.1434349, and our 95% confidence interval for the intercept is 0.555003, 1.1317936
Confidence (and prediction) intervals for a given X
This focus on individual coefficients is very useful, but it can’t tell us two things: how confident we are in the value of an outcome y for a given x, and what value of y we would predict if we observed another x.
Here’s our sample of size 50 with the regression line overlayed.
ggplot(samp,aes(x,y))+geom_point()+geom_smooth(method=lm,color='gray50')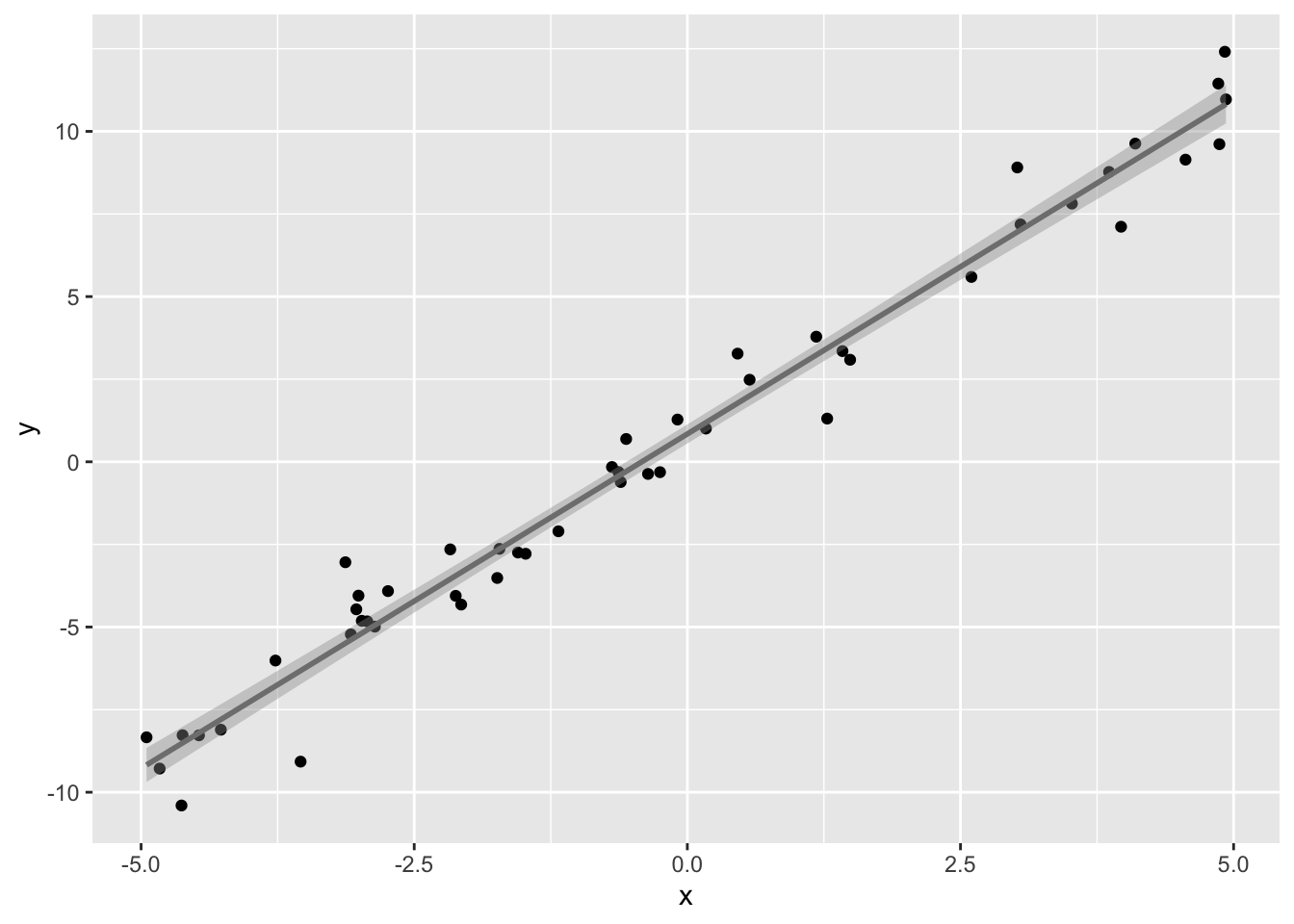
The gray band around the regression line is the 95% confidence interval for ˆy for a given value of x. You can think of it as a range that captures the true regression 95% of the time! It is a band because the interval changes depending on which x you consider. It is narrowest at the point (ˉx,ˉy) and widest at the edges of the data. This confidence interval, for a given value of the predictor xk, is defined as
ˆyk±t∗(n−2)√s2(1n+(xk−ˉx)2∑(xi−ˉx)2),where (as before),s2=∑(yi−ˆy)2n−2
Again, I will not bore you with the derivation of the standard error (it is similar to how we did the slope above). Notice that the standard error is a function of the specific value of xk that is chosen (the numerator of the second term). Notice that this numerator (xk−ˉx)2 will be zero when we choose xk=ˉx, and that the further away xk is from the the mean, the larger the numerator becomes. This fact accounts for the wider confidence interval at the ends of the range of x and the narrowest interval at the mean of x.
Let’s calculate the 95% CI for three values of xk:min(x),0, and ˉx. The mean of the xs in our data was -0.4246 and the smallest x in our data was -4.95
preds<-predict(samp.lm, newdata=data.frame(x=c(min(samp$x),0,mean(samp$x))),interval='confidence')
print(paste("95% CI for yhat when x=min(x): ","[",round(preds[1,2],3),",",round(preds[1,3],3),"]"))## [1] "95% CI for yhat when x=min(x): [ -9.691 , -8.66 ]"print(paste("95% CI for yhat when x=0: ","[",round(preds[2,2],3),",",round(preds[2,3],3),"]"))## [1] "95% CI for yhat when x=0: [ 0.555 , 1.132 ]"print(paste("95% CI for yhat when x=mean(x):","[",round(preds[3,2],3),",",round(preds[3,3],3),"]"))## [1] "95% CI for yhat when x=mean(x): [ -0.302 , 0.27 ]"We can see this better if we plot these (in red) along with the full 95% confidence bands (in gray) on the regression line and zoom in.
ggplot(samp,aes(x,y))+geom_point()+geom_smooth(method=lm,size=.5,color="black",fill='gray50')+
# scale_x_continuous(limits=c(min(x),mean(x)+1))+
# scale_y_continuous(limits=c(-10,5))+
geom_segment(aes(x=min(x),xend=min(x),y=preds[1,2],yend=preds[1,3]),color="red")+
geom_segment(aes(x=0,xend=0,y=preds[2,2],yend=preds[2,3]),color="red")+
geom_segment(aes(x=mean(x),xend=mean(x),y=preds[3,2],yend=preds[3,3]),color="red")+
coord_cartesian(ylim=c(min(y),4),xlim=c(min(x),mean(x)+.5))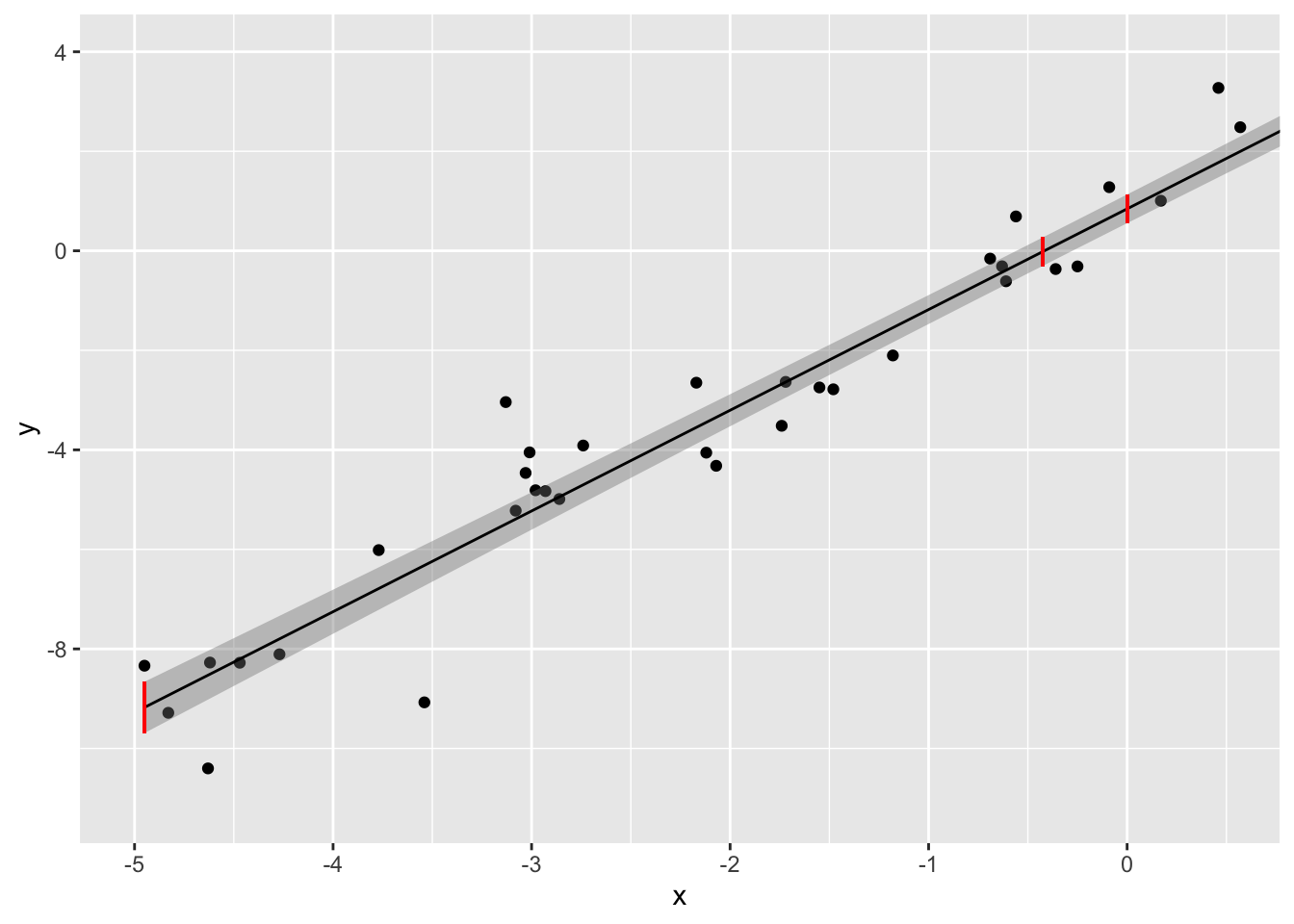
Notice that the 95% CI for ˆy when x=0 is the exact same as the 95% CI for ˆb0! To see this, just plug xk=0 into the formula for the standard error above and compare it with the intercept standard error! They will be identical!
Prediction interval
The confidence intervals we just calculated are for ˆyk=E[y|xk]. But what if we want to predict what yk would actually be if we observed a new xk? These two intervals are not the same: there is a subtle difference! Recall that regression models the distribution of y given x. Thus, even if you knew the true values for b0 and b1, you still don’t know exactly what y itself would be because of the error σ2. Now, ˆyk is definitely your best guess (point estimate), but we are talking the confidence intervals! These are built from the standard error, and the standard error of yk given xk needs to account for the variability of the observations around the predicted mean ˆy (recall: yk∼N(ˆyk,σ2)). Since we don’t have σ2, we use s2. Literally, we are just adding this extra variability into the confidence interval (above) to get our prediction interval:
ˆyk±t∗(n−2)√s2(1+1n+(xk−ˉx)2∑(xi−ˉx)2),where (as before),s2=∑(yi−ˆy)2n−2
Again, the only different between a 95% confidence interval and a 95% prediction interval is the standard error, which is larger for the prediction interval because of the variability of individual observations around the predicted mean (i.e., s2).
Here is the prediction interval for the same values of xk as above:
preds<-predict(samp.lm, newdata=data.frame(x=c(min(samp$x),0,mean(samp$x))),interval='prediction')
print(paste("95% CI for y (obs) when x=min(x): ","[",round(preds[1,2],3),",",round(preds[1,3],3),"]"))## [1] "95% CI for y (obs) when x=min(x): [ -11.26 , -7.092 ]"print(paste("95% CI for y (obs) when x=0: ","[",round(preds[2,2],3),",",round(preds[2,3],3),"]"))## [1] "95% CI for y (obs) when x=0: [ -1.196 , 2.883 ]"print(paste("95% CI for y (obs) when x=mean(x):","[",round(preds[3,2],3),",",round(preds[3,3],3),"]"))## [1] "95% CI for y (obs) when x=mean(x): [ -2.055 , 2.023 ]"Let’s plot both the prediction and the confidence interval for our data:
pred.int<-data.frame(predict(samp.lm, newdata=data.frame(x=samp$x),interval='prediction'))
conf.int<-data.frame(predict(samp.lm, newdata=data.frame(x=samp$x),interval='confidence'))
ggplot(samp,aes(x,y))+geom_point()+geom_smooth(method="lm",size=.5,color="black")+
geom_ribbon(inherit.aes=F,data=conf.int,aes(x=samp$x,ymin=lwr,ymax=upr),fill="red",alpha=.3)+
geom_ribbon(inherit.aes=F,data=pred.int,aes(x=samp$x,ymin=lwr,ymax=upr),fill="blue",alpha=.3)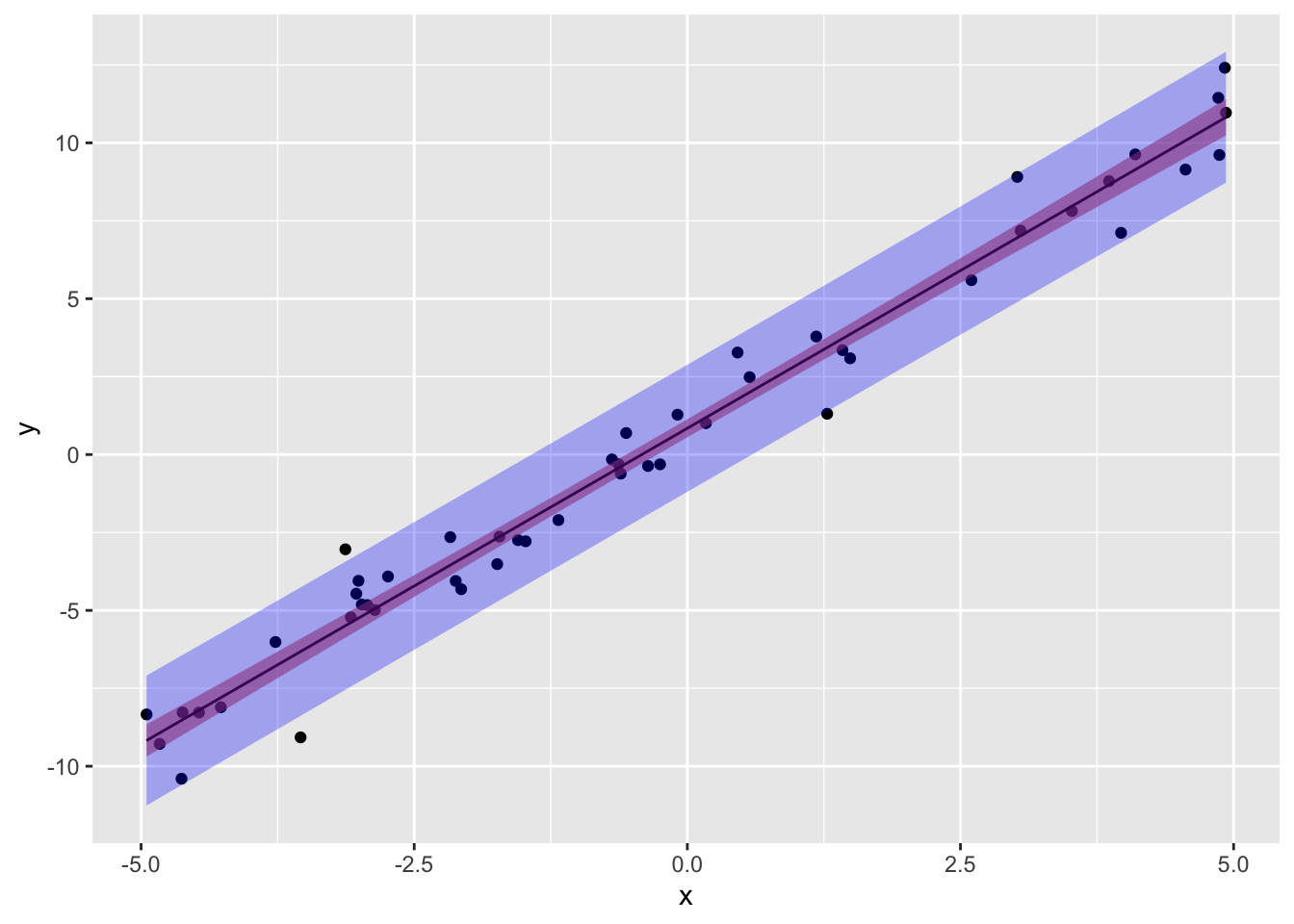
Notice also that the 95% prediction interval captures all but approximately 2-3 observations, which makes sense because we have N=50, since 5% of the time our 95% CI wont contain y, .05∗50=2.5!
What’s the relationship between correlation and regression?
Let’s take a step back from all this nitty-gritty and think about things from an ANOVA perspective. (If you’ve made it this far, you probably won’t need it, but if you want a quick review of ANOVA, check out this post).
In ANOVA, the sum of the squared deviations of the yis around the mean ˉy is the total sum of squares (SST=∑i(yi−ˉy)2). Now, these deviations around the grand mean can be separated into two parts: the variability between the k groups (SSB=∑k(ˉyk−ˉy)2) and the variability within the k groups (SSW=∑k∑i(yki−ˉyk)2). It turns out that SST=SSB+SSW
Analogously, in Regression, the SST=SSR+SSE. For now, instead of groups we have at least one continuous predictor x (we will see soon that ANOVA is a special case of regression). Here, the total sum of squares is the same (SST=∑i(yi−ˉy)2). The regression sum of squares is the part of variability in y attributable to the regression, or the sum of the deviations of the predicted value from the mean of y (SSR=∑i(ˆy−ˉy)2). What’s left over is the error: the deviations of the observed data from the predicted values that lie on the regression line (SSE=∑i(yi−ˆy)2). Thus,
∑i(yi−ˉy)2=∑i(ˆyi−ˉy)2+∑i(yi−ˆyi)2
This says that the total variablity can be partitioned into a component explained by the regression (SSR) and an error component (SSE). A natural question to ask is, what proportion of the variability in y can I account for with my regression ˆb0+ˆb1x+...? To find out, we can literally just look at the ratio SSRSST=∑i(ˆyi−ˉy)2∑i(yi−ˉy)2
Now then, if ˆy=bx, and remembering our formula for variances, we can see that ∑i(ˆyi−ˉy)2∑i(yi−ˉy)2=var(ˆy)var(y)=var(ˆbx)var(y)=ˆb2var(x)var(y)
From above, we have the ˆb=cov(x,y)var(x), so we get ˆb2var(x)var(y)=cov(x,y)2var(x)var(x)2var(y)=cov(x,y)2var(x)var(y)=(cov(x,y)sd(x)sd(y))2=r2
So the proportion of variance explained by the regression line is equal to the square of the correlation coefficient r=cor(x,y)=cov(x,y)/sd(x)sd(y).
Now we are in a position to figure out the relationship between the slope of the regression line ˆb and r.
ˆb=cov(x,y)var(x), r=cov(x,y)√var(x)√var(y) How do we transform r into ˆb? Multiply it by √var(y) and divide by √var(x)! r(√var(y)√var(x))=r(sdysdx)=cov(x,y)√var(y)√var(x)√var(y)√var(x)=cov(x,y)var(x)=ˆbSo,r(sdysdx)=ˆb
We have found that all we need to do is multiply the correlation coefficient between x and y by the standard deviation of y and divide it by the standard deviation of x to get the regression coefficient (from the regression of y on x).
But if regression and correlation are both only able to describe an associative (i.e., non-causal) relationship, why is one different from the other?
Regression is primarily a predictive tool: it tells us what y we can expect in a subset of the observations with given vaules for the predictor variables x (that is, we make a probabilistic prediction by conditioning). To interpret a coefficient estimate causally, the predictor variables need to be assigned in a way that breaks dependencies between them and omitted variables (or noise), either using random assignment or control techniques. Most important from a modeling-flexibility standpoint, regression allows for multiple predictors!
Multiple regression: multiple predictors
So far our focus has been the simple linear case, yi=b0+b1xi+ϵi
By way of transition to the general case, here’s another helpful way of looking at all of this: regression seeks to find the linear combination of the predictor variables x1,x2,... (i.e., b0+b1x1+b2x2,+...) that is maximally correlated with y.
Indeed, minimizing the sum of squared errors is the same thing as maximizing the correlation between the observed outcome (y) and the predicted outcome (ˆy).
This way of thinking allows us to generalize from one predictor of interest to multiple predictors.
ˆyi=b0+b1x1+b2x2+...+bkxkˆzy=β1zx1+β2zx2+...+βkzxk The second equation is the standardized form of the first: they result from estimating the coefficients with standardized variables zy=y−ˉysdy,zx1=x1−ˉx1sdx1,zx2=x2−ˉx2sdx2 etc. Because the variables are scale-free, the coefficients can be easier to interpret and compare. Sometimes you want the interpretation “for ever standard deviation increase in x1, y goes up β1 standard deviations.” Other times you want to keep y and/or the xs in terms of their original units.
It is easy to convert between b and β: you do not need to re-run the regression. As we will see below, b=βsdysdx.
Also, notice that the fully standardized model has no intercept (i.e., β0=0). This will always be the case when all variables are standarized. Just like in simple linear regression, the line (or plane) of best fit passes through the point (y, x_1, …). When all variables are standardized, the mean of each is 0, and so the y-intercept (when zy=0) will be where ˉx1=0 also!
We already saw the matrix equations for calculating our least squares regression weights: ˆb=(X′X)−1X′y. There is another, more direct route to calculate the standardized coefficients ˆβ. All you need are correlations. You need correlations between all pairs of predictors, as well as the correlation between each predictor and the outcome. Specifically,
ˆβ=R−1ry,x[β1β2β3⋮]=[1rx1,x2rx1,x3...rx1,x21rx2,x3...rx1,x3rx2,x31...⋮⋮⋮⋱]−1[ry,x1ry,x2ry,x3⋮]
In the above, R is a correlation matrix containing all pairwise correlations of the predictors. Notice the diagonal consists of 1s because the correlation of anything with itself equals 1.
Here’s some play data
yx1x21216135514127171410ˉy=14ˉx1=8ˉx2=7 Let’s get the deviations and sum their squares
(y−ˉy)2(x1−ˉx1)2(x2−ˉx2)2(−2)2(−7)2(−1)2(−1)2(−3)2(−2)2024202326232SSy=14SSx1=110SSx2=14 …and their products:
(y−ˉy)(x1−ˉx1)(y−ˉy)(x2−ˉx2)(x1−ˉx1)(x2−ˉx2)(−2)(−7)(−2)(−1)(−7)(−1)(−1)(−3)(−1)(−2)(−3)(−2)0(4)0(0)4(0)3(6)3(3)6(3)SPy,x1=35SPy,x2=13SPx1,x2=31
We can compute rx1,x2=∑(x1−ˉx1)(x2−ˉx2)n−1sdx1sdx2=∑(x1−ˉx1)(x2−ˉx2)√∑(x1−ˉx1)2∑(x2−ˉx2)2=SPx1,x2√SSx1SSx2=31√110∗14=0.79
We can do the same for the correlation of each predictor with the outcome:
SPy,x1√SSx1SSy=35√110∗14=0.8919SPy,x2√SSx2SSy=13√14∗14=0.9286
Let’s confirm:
y=matrix(c(12,13,14,17))
x=matrix(c(1,5,12,14,6,5,7,10),nrow=4)
print("Correlation matrix of predictors:")## [1] "Correlation matrix of predictors:"cor(x)## [,1] [,2]
## [1,] 1.0000000 0.7899531
## [2,] 0.7899531 1.0000000print("Correlation of y with x1:")## [1] "Correlation of y with x1:"cor(x[,1],y)## [,1]
## [1,] 0.8918826print("Correlation of y with x2:")## [1] "Correlation of y with x2:"cor(x[,2],y)## [,1]
## [1,] 0.9285714Yep! Looks good! Now for the amazing part:
[β1β2]=[1.79.791]−1[.8919.9286]=11−.792[1−.79−.791][.8919.9286]=[2.6598−2.1011−2.10112.6598][.8919.9286]=[0.42120.5959]
Let’s check our calculations with R
solve(cor(x))%*%cor(x,y)## [,1]
## [1,] 0.4211851
## [2,] 0.5958549Good, it checks out! Now, are these the same as the standardized regression coefficients?
round(coef(lm(scale(y)~scale(x)))[2:3],4)## scale(x)1 scale(x)2
## 0.4212 0.5959#summary(lm(scale(y)~scale(x)))Yep! Neat!
Now that we’ve done the heavy lifting with the matrix equations, I want to show you a really handy (and conceptually important!) way to calculate the standardized regression coefficients using only correlations among x1,x2, and y
Recall that in the simple, one-predictor linear regression (with standardized variables) we had
zy=ry,x1zx1
Now, in the two-predictor case, instead of rx,y we have
zy=β1zx1+β2zx2
You might ask: How is ry,x1 related to β1? Well,
β1=ry,x1−ry,x2rx1,x21−r2x1,x2β2=ry,x2−ry,x1rx1,x21−r2x1,x2 Look at the formula for a minute.
Starting in the numerator, we have ry,x1, the old slope in the single-predictor case. But we subtract off the other slope ry,x2 to the extent that x2 is correlated with x1.
In the denominator, we see r2x1,x2. This is the proportion of variance in x1 shared with x2: their overlap! Thus, the denominator is adjusted to remove this overlap.
In summary, we can see that the old slopes have been adjusted to account for the correlation between x1 and x2.
Let’s show that these actually work. Recall from above that ry,x1=.8919, ry,x2=.9286, and rx1,x2=.79. Plugging in, we get
β1=.8919−(.9286)(.79)1−.792=.4211β2=.9286−(.8919)(.79)1−.792=.5959
Also, we saw that in the simple, two-variable case, b=r(sdysdx). But what about now, when we have two predictors x1 and x2? How can we get unstandardized coefficients (ˆb1,ˆb2) from our standardized ones (ˆβ1,ˆβ2)? Above, we found that
ˆzy=0.4212×zx1+0.5959×zx2
We can just apply the same logic to convert to unstandardized coefficients!
b1=β1(sdysdx1), b2=β2(sdysdx2)
And the intercept can be found using the coefficients by plugging in the mean of each variable and solving for it: b0=ˉy−(b1ˉx1+b2ˉx2)
ˆy=b0+β1(sdysdx1)x1+β2(sdysdx2)x2ˆy=b0+0.4212(sdysdx1)x1+0.5959(sdysdx2)x2Using SS from table above,ˆy=b0+0.4212(√14/3√110/3)x1+0.5959(√14/3√14/3)x2=b0+0.1503x1+0.5959x2 OK, but what about the intercept b0? We know that ˉy=14, ˉx1=8, and ˉx2=7 (see table above). Since the mean value (ˉx1,ˉy) will always been on the line (or in this case, plane) of best fit, we can plug them in and solve for b0
ˉy=b0+0.1503(ˉx1)+0.5959(ˉx2)14=b0+0.1503(8)+0.5959(7)b0=14−1.2024−4.1713=8.6263
So our final (unscaled) equation becomes
ˆy=8.6263+0.1503(x1)+0.5959(x2)
Let’s see if R gives us the same estimates:
coef(lm(y~x))## (Intercept) x1 x2
## 8.6269430 0.1502591 0.5958549Looks good!
Multiple R and R2
Recall that earlier we saw that the proportion of variance in the outcome (y) explained by the predictor was R2=SSregressionSStotal. We found that this was just the Pearson correlation between x and y, rx,y, squared. But now we have two predictors! So what is R2?
Just as r represents the degree of association between two variables, R represents the degree of association between an outcome variable and an optimally weighted linear combination of the other variables. Since the fitted values ˆy represent this best-fitting linear combination of the xs, we could just use that (i.e., R=ry,ˆy). However, there is another formula I want to call your attention to:
R=Ry,12=√r2y,x1+r2y,x2−2ry,x1rx1,x21−r2x1,x2=√β1ry,x1+β2ry,x2 Let’s see it at work:
R=√.4211(.8919)+.5959(.9286)=.9638
It turns out that the proportion of variance in y shared with the optimal linear combination of x1 and x2 is R2=.96382=.9289.
Above we claimed that the correlation coefficient R is the same as the correlation between the fitted values ˆy and the actual values y. Let’s see for ourselves:
#R
cor(y,lm(y~x)$fitted.values)## [,1]
## [1,] 0.9638161#R squared
cor(y,lm(y~x)$fitted.values)^2## [,1]
## [1,] 0.9289415The better the regression line fits, the smaller SSres (This picture from wikipedia illustrates this nicely).
As we discussed above, the sum of squared deviations of y from its mean ˉy (SStot) can be paritioned into a sum of squared deviations of the fitted/predicted values ˆy from ˉy (the SSregression) and the leftover deviations of y from the fitted values ˆy (the SSresiduals, or error).
Because SSreg is the sum of squared residuals after accounting for the regression line, SSregSStot gives the proportion of the error that was saved by using the regression line (i.e., the proportion of variance explained by the regression line).
Is this value (R2=0.9289) the same as R2=SSregressionSStotal=1−SSresidualsSStotal?
R2=SSregressionSStotal=∑(b0+b1x1+b2x2−ˉy)2∑(y−ˉy)2=∑(ˆy−ˉy)2∑(y−ˉy)2=1−∑(y−ˆy)2∑(y−ˉy)2
yϵ=y−ˆyˆy= b0+b1x1+b2x212−.352312.3523=8.6263+0.1503(1)+0.5959(6)13.642512.3573=8.6263+0.1503(5)+0.5959(5)14−.601014.6012=8.6263+0.1503(12)+0.5959(7)17.310916.6895=8.6263+0.1503(14)+0.5959(10)∑ϵ2=.995
So R2=1−SSresidualsSStotal=1−∑(y−ˆy)∑(y−ˉy)=1−.99514=.9289
Yep! 92.9% of the variability in y can be accounted for by the combination of x1 and x2.
An easier way to think about this calculation is to break up our variance like so:
sd2y⏞variance of y=sd2ˆy⏞variance of fitted values+sd2y−ˆy⏞variance of residuals It is mathematically equivalent, but I find the formula rather helpful!
R2 in one bang using correlation matricies
Before we begin our discussion of semipartial and partial correlations, I want to show you a simple matrix calculation of R2 that only requires the correlation matrix of the predictors R and the vector containing each predictor’s correlation with the outcome, rx,y=[ry,x1ry,x2...]T
Recall that above, we had this formula for the standardized regression coefficients:
ˆβ=R−1ry,x[β1β2β3⋮]=[1rx1,x2rx1,x3...rx1,x21rx2,x3...rx1,x3rx2,x31...⋮⋮⋮⋱]−1[ry,x1ry,x2ry,x3⋮] If we (matrix) multiply both sides of this equation by rTx,y=[ry,x1ry,x2...], something really neat happens. I’ll shorten the depictions to the two-predictor case, but the formula holds in general:
rTx,yˆβ=rTx,yR−1ry,x[ry,x1ry,x2...][β1β2⋮]=[ry,x1ry,x2...][1rx1,x2...rx1,x21...⋮⋮⋱]−1[ry,x1ry,x2⋮]ry,x1β1+ry,x2β2=[ry,x1−ry,x2rx1,x21−r2x1,x2−ry,x1rx1,x2+ry,x21−r2x1,x2][ry,x1ry,x2]=r2y,x1−ry,x2rx1,x2ry,x11−r2x1,x2+−ry,x1rx1,x2ry,x2+r2y,x21−r2x1,x2=r2y,x1+r2y,x2−2ry,x2rx1,x2ry,x11−r2x1,x2=R2
All of these are equal to R2! Specifically R2 is equal to the sum of the products of the correlation of y with each predictor times the standardized coefficient for that predcitor (in the two-variable case, R2=ry,x1β1+ry,x2β2). R2 also equals the sum of the univariate r2s minus twice the product of all three unique correlations (2ry,x2rx1,x2ry,x1), divided by the variance not shared by the predictors (1−r2x1,x2).
Don’t believe me?
coryx<-matrix(c(cor(y,x[,1]),cor(y,x[,2])))
corxx<-cor(x)
#as before, the correlation of y with each x
coryx## [,1]
## [1,] 0.8918826
## [2,] 0.9285714#and the correlation matrix of the xs
corxx## [,1] [,2]
## [1,] 1.0000000 0.7899531
## [2,] 0.7899531 1.0000000#now, R2 should be equal to
t(coryx)%*%solve(corxx)%*%coryx## [,1]
## [1,] 0.9289415#we should also be able to get it from the betas like so
t(coryx)%*%coef(lm(scale(y)~scale(x)))[2:3]## [,1]
## [1,] 0.9289415#perfect!Semipartial and Partial Correlations
The R2 value is extremely informative, but you might want to know how much of the variability in y is due to x1, holding x2 constant. This is known as a semi-partial (or “part” but not “partial”) correlation. We will represent this as ry(x1|x2). This is the correlation between x1 and y with the effect of x2 removed from x1 (but not from y1).
On the other hand, we could remove the effect of x2 from both y and x1 before we calculate the correlation. This would result in the partial correlation of x1 and y, which we will denote ry,x1|x2.
The difference between semi-partial and partial correlations can be difficult to see at first, so let’s look at this helpful venn diagram:

Imagine that the variance of each variable is represented by a circle with an area of 1. The overlapping area of x1, x2, and y (A+B+C) is R2. Interestingly, the squared correlation of x1 and y, r2y,x1 (or equivalently, the r2 of the regression of y on x1) is A+C. Likewise, the r2y,x2=B+C
The section marked A is the variance of y shared uniquely with x1, and the section marked B is the variance of y shared uniquely with x2. These represent the square of what is known as the semipartial (or “part”) correlations (that is, A=r2y,x1|x2 and B=r2y,x2|x1).
Notice that when we remove the effect of x2, the squared semipartial correlation of x1 with y is AA+B+C+D=A1=A.
Here is a full table of the relationships in the Venn diagram:
correlation (r)semipartial (sr1)partial pr1=r2y,x1=A+CA+B+C+D=F−FB−FCA+D=r2y,x1|x2=AA+D=F−FB−GBA+D=r2y|x2,x1|x2=AA+B+C+D=A
These squared semipartials are useful: they are equal to the increase in R2 when the second predictor is added to the model. This makes them easy to calculate: to find A above, all we need is r2y,x1|x2=R2−r2y,x1. To find B, r2y,x2|x1=R2−r2y,x1.
For example, we know from above that R2=.9289 and ry,x2=.9286, so A=r2y,x1|x2=.9289−.92862=.0666. Also, since ry,x1=.8919, B=r2y,x2|x1=.9289−.89192=.1334. We can say that 6.66% of the variance in y is shared uniquely with x1 and that 13.34% of the variance in y is shared uniquely with x2.
There is also a useful formula for calculating these semipartial correlations directly with just three values: ry,x2=.9286, ry,x1=.8919, and rx1,x2=.79
sr1=ry,x1|x2=ry,x1−ry,x2rx1,x2√1−r2x1,x2=.8919−.9286(.79)√1−.792=.1583.6131=.2582(=√.0666)
Semipartial correlations: the residuals approach
If you thought that semipartial correlations were confusing, this might help conceptually.
We said at the start that semipartial correlations represented the correlation of y with x1 when the effects of x2 have been removed from x1. To remove the effects of x2 from x1, we regress x1 on x2 (that is, treating x1 as the dependent variable), and we save the residuals (the part of x2 unexplained by x2). Then we correlate these x1 residuals (with the effect of x2 removed) with y to get our semipartial correlation:
res_x1.x2<-lm(x[,1]~x[,2])$res
cor(res_x1.x2,y)## [,1]
## [1,] 0.2582569Semipartial correlations are called semi-partial because the effect of a controlling variable (e.g., x2) is removed from the predictor (x1) but not from the outcome (y). To the get partial correlation, we just remove the effect of the controlling variable from the outcome too! Let’s represent the partial correlation of y and x1 (with the effect of x2 removed from both y and x1) as pr=ry|x2,x1|x2. When we square partial correlations, we get the proportion of variance in y not associated with x2 that is associated with x1.
In the Venn diagram above, this quantity is found by
pr21=r2y|x2,x1|x2=aa+d=R2−r2y,x21−r2y,x2
Because we are completely removing variance from y, the denominator of partial correlations will be smaller than for semi-partial (which includes all of the variance in y). Thus, partial correlations will always be greater than semipartial correlations. Partial and semipartial correlations sr1 and pr1 will only ever be equal to each other if the other predictor x2 is uncorrelated with y (i.e., if ry,x2=0). We can see this using this formula for the partial correlation:
pr1=ry|x2,x1|x2=ry,x1−ry,x2rx1,x2√1−r2x1,x2√1−r2y,x2if ry,x2=0,=ry,x1√1−r2x1,x2(which equals sr1 when ry,x2=0)
Let’s go ahead and use this formula and our correlations to calculate the partial correlation between y and x1, removing the effect of x2 from each. We will need ry,x2=.9286, ry,x1=.8919, and rx1,x2=.79
pr1=ry|x2,x1|x2=ry,x1−ry,x2rx1,x2√1−r2x1,x2√1−r2y,x2=.8919−.9286(.79)√1−.792√1−.92862=.1583.6131∗.3711=.6958
Increments to R2 when adding predictors
It is important to realize that you can build R2 from semipartial correlations. You may have noticed this already, but take a look:
R2=r2y,x1+r2y,x2|x1+r2x3|x1,x2+...
First, using our running example, we can take squared correlation of y with x2 (ry,x2=.92862=.8623) and then add to it the squared semipartial correlation of x1 and y with the effect of x2 removed, r2y,x1|x2=.25822=.0666.
R2=.8623+.0666=.9289
The take-home here is that you can keep on adding variables in this fashion! When you add a new predictor, if it has a correlation with y when you have removed the effects of the other predictors in the model, then R2 will increase by the square of the semipartial correlation!
Let’s look at what happens when we add a third predictor. Unfortunately, because there are only four data points and we are estimating four parameters (including the intercept), we will be able to predict the data perfectly (serious overfitting, leaving no residuals). So we need another observation on each variable too.
yx1x2x31216213554141276171410824181725ˉy=16ˉx1=10ˉx2=9ˉx3=10 First, let’s find r2y,x1 by regressing y on x1 (and confirm that this equals the square of ry,x1 and also the square of the correlation between y and the fitted values ˆy):
x=matrix(cbind(x,c(2,4,6,8)),nrow=4)
x=matrix(rbind(x,c(18,17,25)),nrow=5)
y<-matrix(rbind(y,24),nrow=5)
summary(lm(y~x[,1]))$r.squared## [1] 0.7404815cor(y,x[,1])^2## [,1]
## [1,] 0.7404815cor(lm(y~x[,1])$fitted.values,y)^2## [,1]
## [1,] 0.7404815Check! r2y,x1=.7405. Now we need the semipartial correlation of y and x2 (with the effect of x1 removed from x2), ry,x2|x1. An easy way is to (1) regress x2 on x1 and take the residuals (the part of x2 not associated with x1), and use them to predict y.
res_x2_x1<-lm(x[,2]~x[,1])$residuals
summary(lm(y~res_x2_x1))$r.squared## [1] 0.2432009#correlation of y with the residuals, quantity squared
cor(y,lm(y~res_x2_x1)$fitted.values)^2## [,1]
## [1,] 0.2432009OK, so r2y,x1=.7405 and r2y,x2|x1=.2432, and their sum is .9837. Clearly there is not much additional variability for the third predictor to explain.
But how can we find the third predictor’s contribution to R2, ry,x1|x2,x3?
The same way as before: remove the effects of x1 and x2 from x3 and see how much variability those residuals share with y.
res_x3_x1x2<-lm(x[,3]~x[,1]+x[,2])$residuals
summary(lm(y~res_x3_x1x2))$r.squared## [1] 0.008596529All together,
R2=R2y.123=r2y,x1+r2y,x2|x1+r2y,x3|x1,x2=.7405+.2432+.0086=.9923
We can confirm that this is the total R2 with the full regression:
round(summary(lm(y~x[,1]+x[,2]+x[,3]))$r.squared,4)## [1] 0.9923Notice that it is easy to find squared semipartial correlations by subtracting R2 from different models.
For example, let’s find how much variability in y is shared with x1 when you remove the effects of x2 and x2 (i.e., r2y,x1|x2,x3). As we will see, this is equivalent to the increase in R2 when you add x1 to the regression predicting y that already contains x2 and x3. We can use this logic and work backwards: first, we find the R2 when all three predictors are in the model (we can denote this R2y.123), and subtract from it the R2 when only predictors x2 and x3 are in the model (R2y.23). What you are left with will be r2y,x1|x2,x3. Again,
r2y,x1|x2,x3=R2y.123−R2y.23
Don’t take my word for it. Let’s try it!
Here’s the R2 when all three predictors are in the model (R2y.123):
summary(lm(y~x[,1]+x[,2]+x[,3]))$r.squared## [1] 0.992279And here’s the R2 when just predictors x2 and x3 are in the model (R2y.23):
summary(lm(y~x[,2]+x[,3]))$r.squared## [1] 0.9876434Thus, r2y,x1|x2,x3=R2y.123−R2y.23=.9923−.9876=.0047 This means that when x1 is added to a model that already contains x2 and x3, the increase in R2 is very small: it explains just 0.5% of the additional variability!
But we saw earlier that when x1 is the only predictor in the model, R2=r2y,x1=.7405. With no other predictors in the model, x1 accounts for almost 75% of the variability in y!
This is because the predictors are highly intercorrelated: they share a lot of variance!
Multicollinearity
Multicollinearity is observed when a given predictor can be predicted from the others very accurately. For example, using the data above, the R2 from the model predicting x3 from x1 and x2 (call it r2x3.12) is
summary(lm(x[,3]~x[,1]+x[,2]))$r.squared## [1] 0.9473233Extremely high! This is the reason that x3 adds so little when added to a model containing x1 and x2: it is almost entirely redundant with those variables!
Multicollinearity affects cofficient estimates by making them less precise (large standard errors). This is because collinear predictors contain mostly the same information about the dependent variable y and are thus extremely sensitive to the presence of other predictors. Regression coefficients are interpreted as the impact of one variable (e.g., x1) with the other variables held constant. But because of multicolinearity, we do not have a set of observations for which changes in x1 are independent of changes in the other variables!
Measuring multicollinearity for a variable (say x3) is often done using the tolerance (1−r2x3.12). Here, tolerance=.053. More commonly, the inverse of the tolerance (known as the variance inflation factor, or VIF) is used. VIF=1tolerance=1.053=18.87 Here, this VIF for predictor x3 is very high. Common cut-offs for problematic variables are 5 (conservative) or 10 (liberal).
Regression assumptions
I have already mentioned all of the assumptions of linear regression in this post, but I will bring them all in once place here!
- Linear relationship
- Independent observations (or equivalently, errors)
- Normally distributed errors
- Homoskedasticity (constant variance)
- No outliers (haven’t discussed)
- No severe multicolinearity (e.g., VIF>5)
Partial correlations
Finding the partial correlation from residuals is easy: we do just as we did for semipartials, except we also have to remove the effect of x2 from y. The full procedure is as follows: regress y on x2 and save the residuals ϵy|x2; regress x1 on x2 and save the residuals ϵx1|x2. Finally, compute the correlation between both sets of residuals (i.e., rϵy|x2,ϵx1|x2).
res_x1.x2<-lm(x[,1]~x[,2])$res
res_y.x2<-lm(y~x[,2])$res
cor(res_x1.x2,res_y.x2)## [1] 0.4785116Thus, we can say that pr21=.69582=48.4% of the variance in y is uniquely associated with x1.
Let’s say y is a vector of i people’s scores on an survey measuring attitude toward abortion, x1 is a vector of political ideology scores, and x2 is a vector of religiosity scores. Clearly the outcome would be correlated with each of the variables in isolation, but what if we want to model y as a function of both? Regression allows us to assess the unique relationship between a predictor and an outcome variable conditional on other predictors.
For example, the relationship between political views (x) and abortion attitudes (y) may appear strong, but if removing the effect of religiosity (z) from both leaves little or no variation in common (i.e., the partial correlation ry,x|z is near zero; see below), then the influence of x on y is likely spurious, since it no longer exists given z. Another way to think about the relationship of x and y “controlling for” z is to look at the relationship of x and y only in groups that have the same value for z
